 |
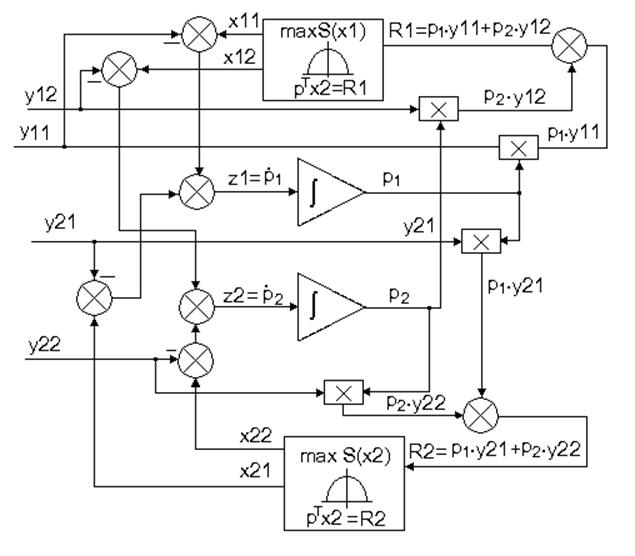
Структура модели динамического рынка с двумя ценами и двумя участниками представлена на рис.1. Два экстремальных блока находят максимумы функций полезности S1(x1) и S2(x2), выдавая на выходы решения экстремальной задачи: составляющие векторов потребления: х11,х12 и х21,х22. На входы экстремальных блоков поступают бюджетные ограничения: R1 и R2, зависящие от цен. Два интегратора формируют цены на первый и второй товары, на каждом из интеграторов устанавливают начальные условия, соответствующие ценам открытия рынка. На входы интеграторов поступают соответствующие координаты вектора z- вектора избыточного спроса или предложения (в зависимости от знака). На вход рынка поступают предложения товаров от первого и второго участников рынка в виде соответствующих координат вектора y.
Задача анализа такой
системы достаточно сложна. Однако можно использовать то свойство, что ![]() , т.е.
вектор избыточного спроса или предложения зависит только от соотношения между
ценами. Введем новую переменную
, т.е.
вектор избыточного спроса или предложения зависит только от соотношения между
ценами. Введем новую переменную 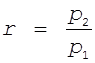 , тогда координата вектора z, например z2,
будет зависеть от переменной r, т.е. можно записать, что z2 = f(r), где f(r)-
некоторая функция от r. Запишем закон Вальраса для случая двух цен:
, тогда координата вектора z, например z2,
будет зависеть от переменной r, т.е. можно записать, что z2 = f(r), где f(r)-
некоторая функция от r. Запишем закон Вальраса для случая двух цен: ![]() . Подставляя
в это уравнение z2 = f(r) и деля его левую и правую части на
. Подставляя
в это уравнение z2 = f(r) и деля его левую и правую части на ![]() , получаем
выражение для другой координаты вектора z:
, получаем
выражение для другой координаты вектора z:
![]() . Запишем
дифференциальное уравнение для переменной r, взяв производную
. Запишем
дифференциальное уравнение для переменной r, взяв производную
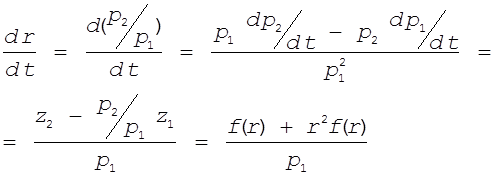
Кроме того, учтем, что ![]() или
или 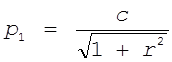 и
и
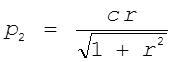 .
Тогда
.
Тогда
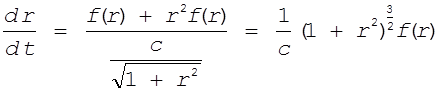 .
Получаем нелинейное дифференциальное уравнение относительно одной переменной r.
.
Получаем нелинейное дифференциальное уравнение относительно одной переменной r.
Для анализа этого уравнения необходимо найти математическую зависимость f=f(r). Для этого надо задать конкретный вид зависимостей функций полезности участников рынка от их векторов спроса. Пусть первый участник рынка имеет функцию полезности S1 = x11∙x12, а второй S2 = x21² ∙x22, а начальные запасы товаров y11 = 10, y12 = 15, y21 = 30, y22 = 15. Цены открытия рынка р1(0) = 3, р2(0) = 4.
Ранее мы приняли, что f(r) = z2(p). Поэтому найдем, чему равняется z2(r). Сначала определим z2 . С учетом нашим обозначений - это вторая координата вектора избыточного спроса (или предложения), которая равна
z2 = x12+x22-y12-y22 = x12+x22 -15-15= x12+x22-30
Следовательно. необходимо определить, как зависят от r координаты x12 и x22. Возьмем уравнение бюджетных ограничений для первого участника рынка:
p1∙x11+р2∙x12= p1∙y11+р2∙y12
и подставим в него цену р2, выраженную через р1, т.е. р2 = r∙р1. Получаем
p1∙x11+ r∙р1∙x12= p1∙y11+ r∙р1∙y12.
Сокращая левую и правую части на р1, получаем
x11+ r∙x12= y11+ r∙y12.
Отсюда находим зависимость x11 от r:
x11= y11+ r∙y12- r∙x12.
Подставляя это соотношение в первую функцию полезности, получаем
S1 = (y11+ r∙y12- r∙x12)∙x12.
Максимизируем функцию полезности, т.е. найдем производную и приравняем нулю:
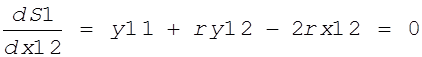 .
.
Отсюда находим x12:
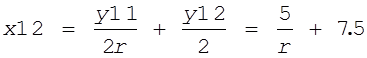 .
.
Возьмем второе уравнение бюджетных ограничений (для второго участника):
p1∙x21+р2∙x22= p1∙y21+р2∙y22
и аналогично подставим в него цену р2, выраженную через р1, т.е. р2 = r∙р1. Получаем
p1∙x21+ r∙р1∙x22= p1∙y21+ r∙р1∙y22.
Сокращая левую и правую части на р1, получаем х21+ r∙x22= y21+ r∙y22.
Отсюда находим зависимость x21 от r:
х21= y21+ r∙y22- r∙x22.
Подставляя это соотношение во вторую функцию полезности, получаем
S2 = (y21+ r∙y22- r∙x22)²∙x22.
Максимизируем функцию полезности, т.е. найдем производную и приравняем нулю:
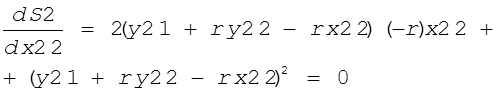 .
.
Выносим за скобку общий множитель:
(y21 +ry22-rx22)(-2rx22+ y21 +ry22-rx22)=0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.