Динамическая модель рынка (Модель К.Эрроу и Л.Гурвица), страница 4

Тогда приравнивая поочередно выражения в обеих скобках нулю, получаем:

y21 +ry22-rx22=0

y21 +ry22-3rx22=0

Отсюда находим два решения для  x22:

.

.

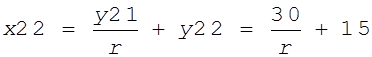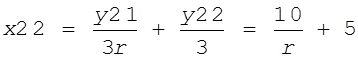Очевидно, одно из этих решений дает точку максимума, а другое - точку минимума. Для определения характера точек экстремума можно взять вторую производную от целевой функции и посмотреть ее знак в точке экстремума. Этого делать не будем, просто найдем вторую координату х21 для двух значений х22:

х21= y21+ r∙y22- r∙x22=30+15r-30-15r=0

х21= y21+ r∙y22- r∙x22=30+15r-10-5r=20+10r

Так как S2 = x21² ∙x22, то второе решение для х21 и х22 всегда, при любом r>0, дает значение S2 больше, чем первое решение, которое дает S2=0.

Теперь уже можно записать, как z2 зависит от r:

z2= x12+x22-25=.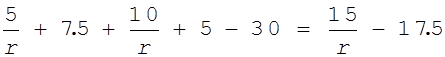

Следовательно,  f(r) = z2=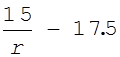.  Подставляем функцию f(r) в дифференциальное уравнение для нахождения r:

. 

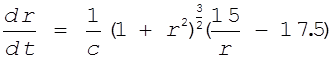Теперь задавая начальное значение для переменной 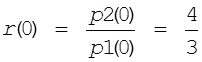, можно, решив дифференциальное уравнение, найти характер изменения цен во времени от открытия рынка до установления состояния равновесия.

Найдем состояние равновесия рынка, приравняв производную в левой части дифференциального уравнения нулю:

.

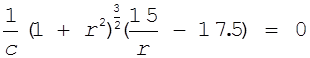Видно, что рынок имеет одно состояние равновесия, поскольку только второй сомножитель может быть равен 0:

.

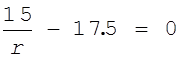Следовательно, состояние равновесия определяется значением r = 6/7  или p2 = p1∙6/7. Постоянная C находится из соотношения , которое справедливо и для начальных цен открытия рынка ( цены всегда на поверхности сферы), поэтому

С²=3²+4²=25. Определяем цены в равновесном состоянии:

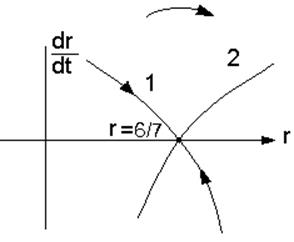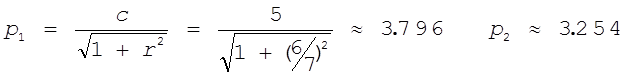
Устойчивость состояния равновесия проверяем  методом фазовых траекторий (рис.2)

Рис.2

Так как кривая 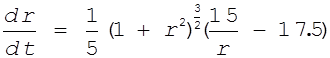 имеет один корень (r =6/7), то она пересекает ось абсцисс только в одной точке при r = 6/7. Возможны только два варианта наклона этой кривой: 1 и 2. Устремим координату r к + ∞, тогда

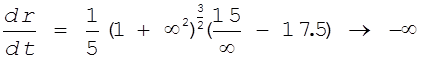, для этих условий подходит только кривая 1. По правилам прохождения фазовых траекторий расставляем на кривой 1 направления движения стрелками. Видно, что точка r = 6/7 является точкой устойчивого равновесия.

По приведенным выше формулам рассчитаны значения координат векторов спроса первого и второго участников рынка в точке равновесия:

x12=7.5+5/r= 13.333,

x11= y11+ r∙y12- r∙x12=11.429,

x21=20+10r=28.571,

x22=5+10/r=16.667.

Проверим баланс предложения и спроса в точке равновесия.

По первому товаруx11+x21= 11.429+28.571=40=y11+y21=10+30=40.

По второму товаруx12+x22= 13.333+16.667=30=y12+y22=15+13=30.

Следовательно, вектор z в точке равновесия является нулевым. Проверим баланс стоимости товаров в точке равновесия.

Для первого участникаp1 ∙ x11+ p2 ∙ x12=3.796∙ 11.429+ 3.254 ∙ 13.333= 86.772

p1 ∙ y11+ p2 ∙ y12=3.796∙ 10+ 3.254 ∙ 15= 86.772

Для второго участникаp1 ∙ x21+ p2 ∙ x22=3.796∙ 28.571+ 3.254 ∙ 16.667= 162.698

p1 ∙ y21+ p2 ∙ y22=3.796∙ 30+ 3.254 ∙ 15=162.698

Решение нелинейного дифференциального уравнения, полученного путем моделирования, для переменной г с выходными сигналами в виде цен p1 и p2 приведено на рис.3.

То же решение с выходными сигналами в виде координат векторов спроса первого и второго участников рынка приведено на рис.4.

                         Рис.3                                                           Рис.4                                                          

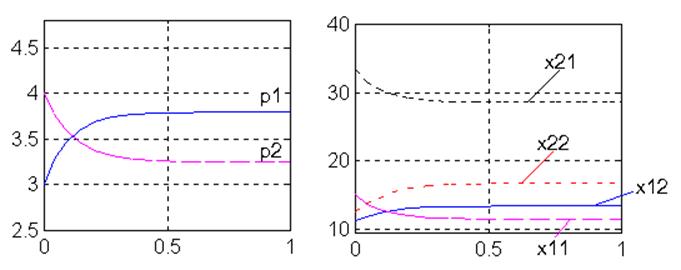Из рис.3 видно, что в процессе торга цены стремятся к установившемуся состоянию равновесия. После установления равновесия производится обмен товарами между участниками рынка.