Динамическая модель рынка (Модель К.Эрроу и Л.Гурвица), страница 2

Определение. Рынок называется устойчивым, если при любых начальных ценах  p  > 0 вектор цен p(t) стремится к равновесному вектору цен.

Сформулируем несколько теорем, относящихся к динамической модели рынка.

Теорема 1 (или закон Вальраса).  Она утверждает, что

.

Доказательство.  Из условия  (2) следует, что 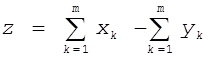. Умножаем слева на вектор . Получаем 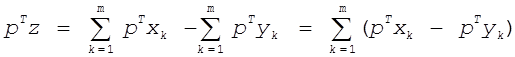. Из условия (1) следует, что . Поэтому  последняя сумма равна нулю и .

Теорема 2. При любом изменении цен конец  n-мерного вектора цен p(t) движется  по поверхности n-мерной сферы.

Доказательство.  Из закона Вальраса следует, что , с другой стороны

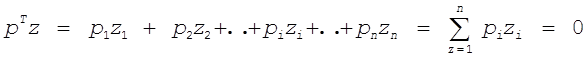.  Так как 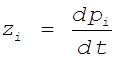, то 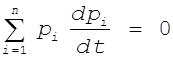   . Возьмем интеграл от левой и правой частей последнего равенства

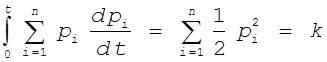, где  к - некоторая константа. Следовательно,

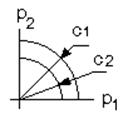
, т.е. получаем уравнение n-мерной сферы с радиусом, равным с. Для частного случая двух цен получаем уравнение окружности.

Ранее мы определяли, что . Отюсюда видно, что с- это радиус сферы движения цен.

Условие устойчивости динамического рынкаДля того, чтобы рынок был устойчивым,  для всякого вектора  равновесных цен должно выполняться условие

.

Доказательство. Пусть  - вектор равновесных цен, а  - вектор начальных цен. Рассмотрим расстояние от  до :      .  Мы хотим показать, что при выполнении условия   расстояние уменьшается при увеличении t. Для этого нужно показать, что уменьшается квадрат этого корня, т.е.

 при  .  Найдем

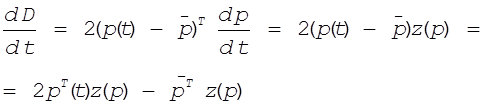
По закону Вальраса , поэтому получаем 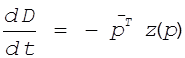 , тогда при условии, что , получаем, что 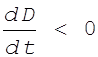. Следовательно, производная от расстояния по времени получается отрицательной, поэтому расстояние уменьшается. и рынок от начального состояния  цен стремится к их равновесному состоянию.

                                      Рынок с двумя ценами

Рассмотрим в качестве примера рынок с двумя видами товаров и, следовательно, с двумя ценами. Так как имеется всего две цены, то вектор z имеет две координаты: z1 и z2. Пусть на рынке действуют два продавца-покупателя: первый и второй. Вектор потребления первого участника обозначим через х1, а вектор предложения - через y1. Вектор потребления второго  участника обозначим через х2, а вектор предложения - через y2. В общем случае участники торгов приходят на рынок с двумя видами товаров (поскольку мы определили, что это рынок с двумя видами товаров и цен) и потребляют (каждый) также эти два вида товаров. Тогда можно записать, что

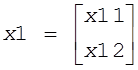,  где х11 - потребление первым участником первого товара, а х12 - потребление первым участником второго товара; 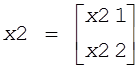, где х21 - потребление вторым участником первого товара, а х22 - потребление вторым участником второго товара. Аналогично записываются вектора предложения для обоих участников: 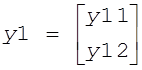, где y11 - предложение первым участником первого товара, 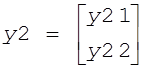, где y21 - предложение вторым участником первого товара,  y22 - предложение вторым участником второго товара. Кроме того, задаются также функции полезности первого и второго участников рынка:  и .

Если первый участник пришел на рынок с одним видом товаров, а другой - с другим, и они хотят обменять их друг на друга, то необходимо обнулить соответствующие координаты в векторах х1,х2,y1,y2, а также задать функции полезности, зависящими только от той координаты вектора х1 или х2, которая нужна первому или второму участнику обмена.

Задача нахождения равновесия  на динамическом рынке, также, как и на статическом рынке, решается как задача определения максимума функций полезности каждого из участников торгов. Только цены будут переменными, изменяющимися во времени и зависящими от избыточного спроса или предложения.