Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Сопротивление материалов»
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА
по дисциплине
«СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»
(за III семестр 2011-2012 уч.года)
по теме:
«Расчёт прямых стержней на прочность»
Вариант Х-Х-Х
Выполнил: ст.гр.
Проверил:
Омск – 2011
Задача №1
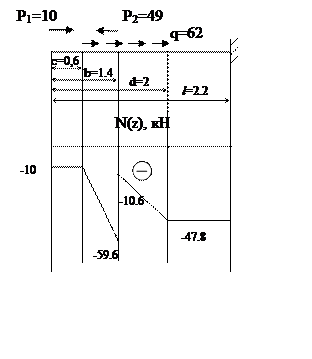 Растяжение - сжатие
Растяжение - сжатие
Уравнение продольной силы:
N(z)=N(0)│I – q(z-0.6)│II + P2│III + q(z-2)│IV
Г.У.: N(0)=P1
Построение эпюр осуществляется по участкам
Условие прочности: σ ≤ [σ],где ![]()
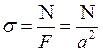 , →
, → 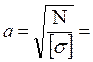
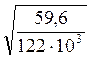 =0.0221 м
=0.0221 м
Из нормального ряда выбираем значение а=24 мм
Опасное сечение z=1,4 м
Нормальные напряжения для выбранного стержня в опасном сечении будут равны:
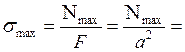
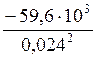 =-103,5 МПа
=-103,5 МПа
Т.к. Nmax < 0, схема нагружения – сжатие , при котором σmax=σ 3 , а σ2=σ 1 =0, следовательно, возникает одноосное (линейное) напряжённое состояние.
Наибольшее касательное напряжение будет действовать в сечении, расположенном под углом 45º к максимальным нормальным напряжениям и определяются по формуле:
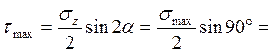 -51,75 МПа
-51,75 МПа
Нормальные напряжения в этом сечении будут равны:
![]() -51,75
МПа
-51,75
МПа
Главные линейные деформации будут определяться из закона Гука:
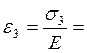 -0,0005175
-0,0005175
![]() 0,00015525
0,00015525
где Е=2·1011Па – модуль Юнга
μ=0,3 – коэффициент Пуассона
Размер сечения после деформации: а1=а(1+ε2)=24,003726 мм
Задача №2
Кручение

Уравнение крутящего момента:
Mк(z)=Мк(0)│I + m(z-0,4)│II + L1│III + L2│IV
Г.У.: Mк(l)= 0 → Mк(0)=-5.04 кН·м
Построение эпюр осуществляется по участкам.
По теории наибольших касательных напряжений: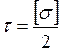 . Касательные напряжения, которые возникают
при кручении, определяются по формуле:
. Касательные напряжения, которые возникают
при кручении, определяются по формуле: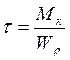 , (где Wρ – полярный момент сопротивления). Таким образом, для
данного стержня можно определить:
, (где Wρ – полярный момент сопротивления). Таким образом, для
данного стержня можно определить: 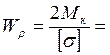
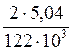 =0.000083
м3
=0.000083
м3
Для круглого сечения:
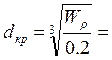
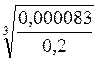 =0,0744 м
=0,0744 м
Из нормального ряда выбираем значение dкр=75 мм
Для кольцевого сечения:
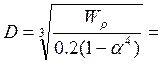
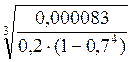 =0,0816 м
=0,0816 м
d=α·D=0,0571 м
Из нормального ряда выбираем значение D=82мм , d=56 мм
Массу выбранных стержней оценим по их площадям:
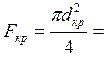 0,00441
м2
0,00441
м2 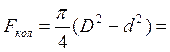 0,00281 м2
0,00281 м2
Т.к. Fкр > Fкол, следовательно, mкр > mкол.
При кручении возникает двухосное напряжённое состояние, т.е. σ1,3=±τ, а σ2=0.
Касательные напряжения определим по формуле:
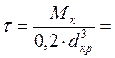
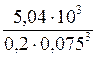 =59,7 МПа
=59,7 МПа
Направление главных напряжений определим через тангенсы углов
tg α1=σ1/τ=τ/τ=1, →α1=45°
tg α3=σ3/τ=-τ/τ=-1, →α3=-45°
Задача №3
Поперечный изгиб
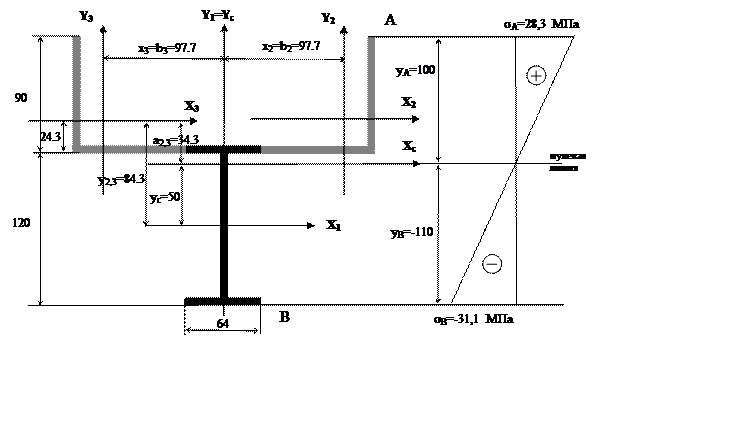
Выписываем из таблиц прокатного сортамента необходимые данные для фигур, составляющих поперечное сечение:
Фигура №1
F1=14,7 см2
Jx1=350 см4
Jy1=27,9 см4
Фигура №2,3
F2,3= 10,6 см2
Jx2,3=82,1см4
Jy2,3=82,1см4
Для определения положения центра тяжести сечения выбираем вспомогательные оси Х1Y1.
xc=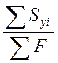 =
=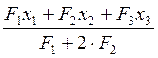 =0
=0
yc=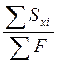 =
=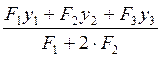 =
=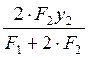 =5 см где x1=0, x2=9.77 см,
х3=-9.77 см;
=5 см где x1=0, x2=9.77 см,
х3=-9.77 см;
y1=0, y2=8.43см, y3=8.43 см.
Отмеряя в осях Х1Y1 координаты (0;yc) находим положение центра тяжести всего сечения. Для определения центральных осевых моментов определим координаты центров тяжести фигур №1,2,3 в системе осей ХсYс:
а1=ус=5 см, а2,3=у2 – ус=3.43 см
b1=хс=0 см, b2=9.77 см, b3=-9.77 см
Используя формулы преобразования при параллельном переносе осей получаем:
Jxc=![]() =(Jx1+a12F1)+(Jx2+a22F2)+(Jx3+a32F3)=(Jx1+a12F1)+2(Jx2+a22F2)=1131см4
=(Jx1+a12F1)+(Jx2+a22F2)+(Jx3+a32F3)=(Jx1+a12F1)+2(Jx2+a22F2)=1131см4
 Jyc=
Jyc=![]() =(Jy1+b12F1)+(Jy2+b22F2)+(Jy3+b32F3)=Jy1+2(Jy2+b22F2)=2216
см4
=(Jy1+b12F1)+(Jy2+b22F2)+(Jy3+b32F3)=Jy1+2(Jy2+b22F2)=2216
см4
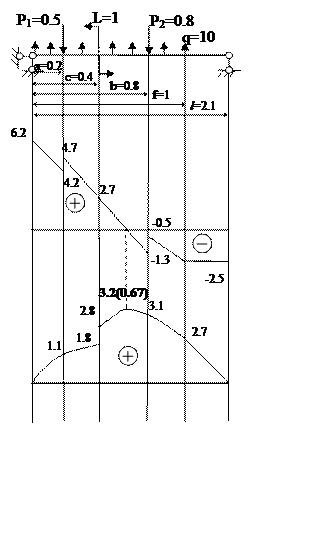 Уравнение поперечных сил:
Уравнение поперечных сил:
Qy(z)=Qy(0) – qz│I + P1│II,III + P2│IV + q(z-1)│V
Уравнение изгибающих моментов:
Mx(z)=Mx(0) + Qy(0)z – qz2/2│I + P1(z-0.2)│II + L│III + + P2(z-0.8)│IV + q(z-1)2/2│V
|
Построение эпюр осуществляется по участкам.
Опасное сечение: z= 0.67 м
|
Нормальные напряжения в этих точках определим по следующим формулам:
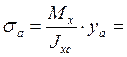
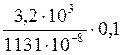 =28,3 МПа
=28,3 МПа
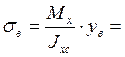
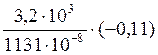 =31,1 МПа
=31,1 МПа
Наибольшие касательные напряжения в поперечном сечении, где действует Qу max, будут действовать на нулевой линии. Определим их по формуле Журавского:
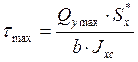
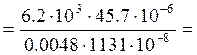 5.2 МПа где Qy max – максимальная
поперечная сила, Qy max =6.2 кН
5.2 МПа где Qy max – максимальная
поперечная сила, Qy max =6.2 кН
b – ширина отсекаемой части, b=4.8 мм
Jхс – главный центральный момент инерции, относительно оси Хс, Jхс=1131 см4
Sх* – статический момент отсечённой части (определяется из чертежа)
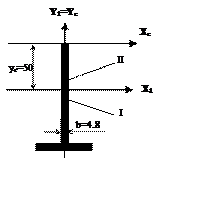 Sх* = SхI*
+SхII*
=Sx + F·yc=33.7 + 0.48·52=45.7 см3
Sх* = SхI*
+SхII*
=Sx + F·yc=33.7 + 0.48·52=45.7 см3
Из исходных данных [σ]=135 МПа
Т.к. [σ] ≥ σа,в; τmax – условие прочности выполняется
Задача №4
Растяжение с изгибом
Вычислим геометрические характеристики поперечного сечения стержня:
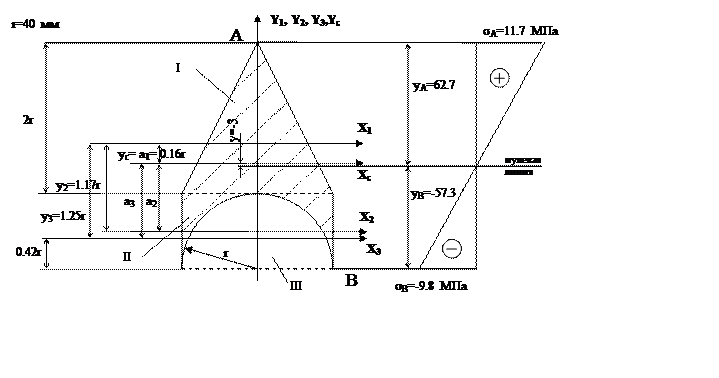
Фигура №1 треугольник
F1= 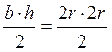 =2r2
=2r2
Jx1=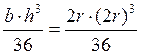 = 0.44r4
= 0.44r4
Jy1=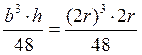 =0.33r4
=0.33r4
Фигура №2
прямоугольник
F2=b·h=2r·r=2r2
Jx2=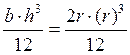 =0.17r4
=0.17r4
Jy2=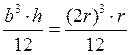 =0.67r4
=0.67r4
Фигура №3 полукруг
F3=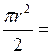 1.57r2
1.57r2
Jx3=0.007d4 =0.112r4
Jy3=0.025d4=0.4r4
Для определения положения центра тяжести сечения выбираем вспомогательные оси Х1Y1.
xc=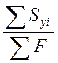 =
=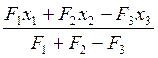 =0; yc=
=0; yc=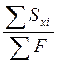 =
=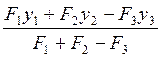 =
=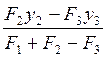 =-0.16r
=-0.16r
где x1=0, x2=0, х3=0;
y1=0, y2=-1.17r , y3=-1.25r .
Отмеряя в осях Х1Y1 координаты (0;yc) находим положение центра тяжести всего сечения. Для определения центральных осевых моментов определим координаты центров тяжести фигур №1,2,3 в системе осей ХсYс:
а1=ус=0.16r, а2=у2 – ус=1.01r, а3=у3 – ус=1.09r; b1=хс=0, b2=0, b3=0
Используя формулы преобразования при параллельном переносе осей получаем:
Jxc=![]() =(Jx1+a12F1)
+ (Jx2+a22F2) – (Jx3+a32F3)=0.72r4
=(Jx1+a12F1)
+ (Jx2+a22F2) – (Jx3+a32F3)=0.72r4
Jyc=![]() =(Jy1+b12F1)
+ (Jy2+b22F2) – (Jy3+b32F3)=0.6r4
=(Jy1+b12F1)
+ (Jy2+b22F2) – (Jy3+b32F3)=0.6r4
![]()
Приведём все силы к оси стержня:
L1=P1·a=0.24 кН·м
P2Z=P2·cos α=0.93 кН
P2Y=P2·sin α=0.36 кН
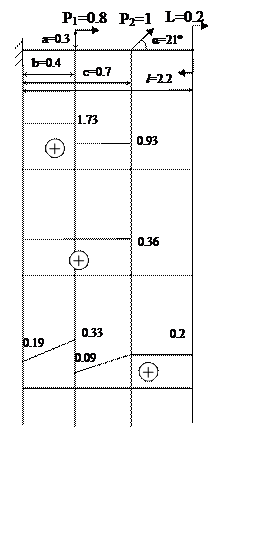
Уравнение продольных сил:
N(z)=N(0)│I – P1│II – P2Z│III
Уравнение поперечных сил:
|
Уравнение изгибающих моментов:
Mx(z)=Mx(0) + Qy(0)z│I – L1│II – P2Y(z-0.7)│III
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.