|
Г.У.:
N(l)=0
Qy(l)=0
|
|
Qy(0)=0.36 кН
Mx(0)=0.19 кН·м
Построение эпюр осуществляется по участкам.
Опасное сечение: z=0.4 м
Уравнение нулевой линии в случае растяжения с изгибом имеет вид:
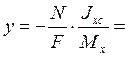
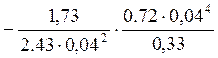 =-0.0025 м
=-0.0025 м
Построим на чертеже поперечного сечения нулевую линию вида у=-3мм. Тогда, координаты крайних точек опасного поперечного сечения будут равны: уa=6.27 см, ув=-5.73 см.
Нормальные напряжения в этих точках определим по следующим формулам:
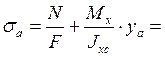 11.7 МПа
11.7 МПа
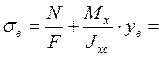 -9.8 МПа
-9.8 МПа
Из исходных данных [σ]=115 МПа
Т.к. [σ] ≥ σа,в – условие прочности выполняется
Задача №5
Косой изгиб
Выписываем из таблиц прокатного сортамента необходимые данные для фигур, составляющих поперечное сечение:
Фигура №1
F1=14.7 см2
Jx1=350 см4
Jy1=27.9 см4
J x1y1=0
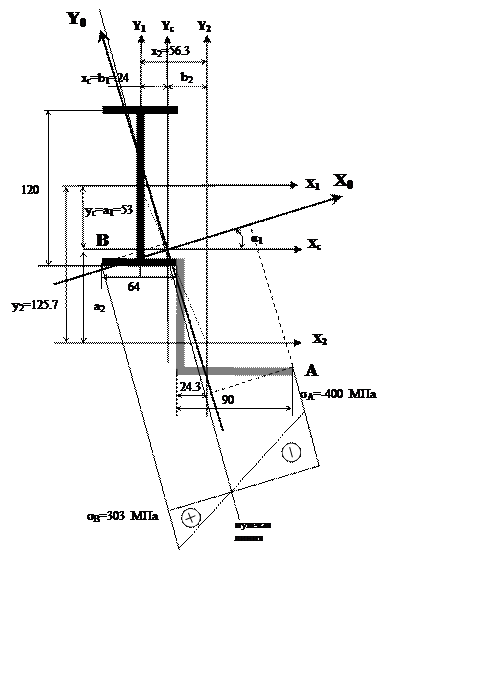 Фигура №2
Фигура №2
F2=10.6 см2
Jx2=82.1 см4
Jy2=82.1 см4
J x2y2=48 см4
Для определения положения центра тяжести сечения выбираем вспомогательные оси Х1Y1.
xc=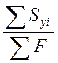 =
=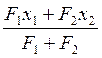 =2.4 см
=2.4 см
yc=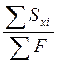 =
=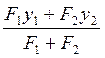 =-5.3 см где x1=0,
x2=5.63 см; y1=0,
y2=-12.57см.
=-5.3 см где x1=0,
x2=5.63 см; y1=0,
y2=-12.57см.
Отмеряя в осях Х1Y1 координаты (хс;yc) находим положение центра тяжести всего сечения. Для определения центральных осевых моментов и центробежного момента инерции сечения определим координаты центров тяжести фигур №1 и №2 в системе осей ХсYс:
а1= ус=5.3 см, а2=у2 – ус=-7.27 см;
b1= хс=-2.4 см, b2=x2 – xс=3.23 см.
Используя формулы преобразования при параллельном переносе осей получаем:
Jxc=(Jx1+a12F1)+(Jx2+a22F2)=1405.3 см4
Jyc=(Jy1+b12F1)+(Jy2+b22F2)=305.3 см4
Jxcyc=(Jx1y1+a1b1F1)+(Jx2y2+a2b2F2)=-387.9 см4
Вычислим главные моменты инерции по формуле:
J1,2=0.5[(Jxc+Jyc)±![]() ]
]
Принимаем J1=Jmax=1528.3 см4, J2=Jmin=182.3 см4
Определим положение главных центральных осей ХоУо по формулам:
tg α1 (Xc,Xo)=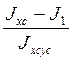 =
0.317 → α1=17.6º
=
0.317 → α1=17.6º
tg α2 (Xc,Yo)=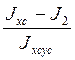 =-3.152
→ α2=-72.4º
=-3.152
→ α2=-72.4º
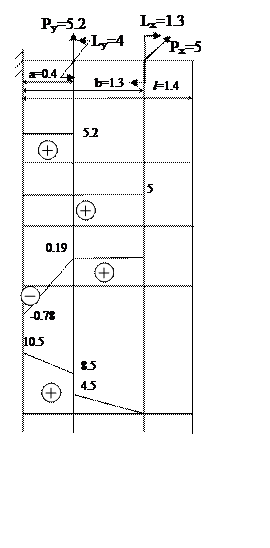 Уравнение поперечных сил:
Уравнение поперечных сил:
Qy(z)=Qy(0)│I – Py│II,III
|
Уравнение изгибающих моментов:
|
||||
|
||||
Mx(z)=Mx(0) + Qy(0)z│I – Py(z-0.3)│II – Lx│III
My(z)=My(0) – Qz(0)z│I – Ly│II + Px(z-0.7)│III
|
Г.У.:
Qy(l)=0
|
|
My(l)=0
Qy(0)=5.2 кН
Qx(0)=5 кН
Mx(0)=-0.78 кН·м
My(0)=10.5 кН·м
|
Опасное сечение: z=0 м
Определим изгибающие моменты относительно главных осей инерции по формулам:
|
|
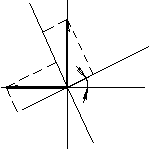 Myо=
Myс·cos α + Mxс·sin α=10.2 кН·м
Myо=
Myс·cos α + Mxс·sin α=10.2 кН·м
|
|||
|
|||
|
|
|
α=17.6º
Уравнение нулевой линии при косом изгибе будет определяться следующим образом:
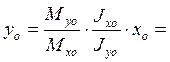
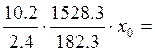 35.6x0
35.6x0
Построим нулевую линию (прямую вида у=kх) в осях ХоУо на чертеже поперечного сечения, определим положение опасных точек и замерим их координаты: А(6.81;-11.76), В(-5.4;0.48) [см]
Нормальные напряжения в этих точках определим по следующим формулам:
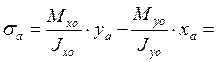 -400 МПа
-400 МПа
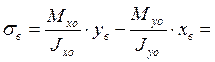 303 МПа
303 МПа
Из исходных данных [σ]=115 МПа
По условию прочности [σ] ≥ σа,в, т.к. [σ] < σа,в – условие прочности не выполняется.
Задача №6
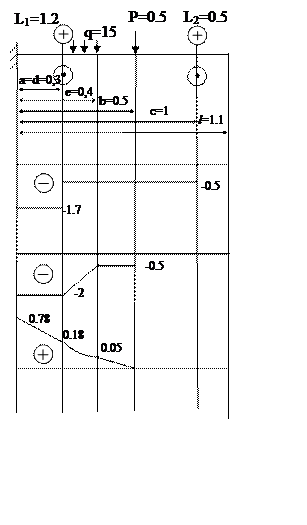 Изгиб с кручением
Изгиб с кручением
Уравнение крутящего момента:
Мк(z)=Мк(0)│I + L1│II-IV + L2│V
Уравнение поперечных сил:
Qy(z)=Qy(0)│I + q(z-0.3)│II – q(z-0.4)│III + P1│IV
Уравнение изгибающих моментов:
Mx(z)=Mx(0) + Qy(0)z│I + q(z-0.3)2/2│II –
|
Г.У.: Mк(l)=0
Qy(l)=0
|
Mк(0)=-1.7 кН·м
Qy(0)=-2к Н
Mх(0)=0.78 кН·м
Построение эпюр осуществляется по участкам.
Опасное сечение: z=0 м
|
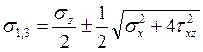 , получаем σэкв=
, получаем σэкв=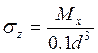 ,
, 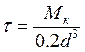 , следовательно, σэкв=
, следовательно, σэкв=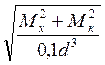 , а с учётом условия прочности состояния σэкв
≤ [σ], получаем формулу для нахождения диаметра круглого поперечного
сечения:
, а с учётом условия прочности состояния σэкв
≤ [σ], получаем формулу для нахождения диаметра круглого поперечного
сечения: 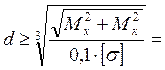
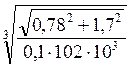 =0,0568 м
=0,0568 м
Из нормального ряда выбираем значение d=58 мм
Для выбранного стержня определим величину и направление главных напряжений в опасной точке. В опасной точке поперечного сечения
Мx max=0,78 кН·м , Мк max=-1,7 кН·м, следовательно,
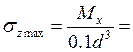 40 МПа
40 МПа
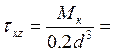 -43,6 МПа
-43,6 МПа
Главные напряжения в этой точке будут равны:
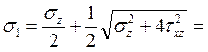 68 МПа,
68 МПа,
![]() ,
,
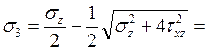 -28 МПа
-28 МПа
Направление главных напряжений определим через тангенсы углов
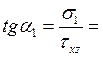 -1,56 → α1=-57,3º
-1,56 → α1=-57,3º
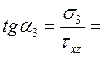 0,64 → α3=32,7º
0,64 → α3=32,7º
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.