Определение крайних (мертвых) положений механизма. Построение планов положений исследуемого механизма. Кинематическое исследование механизма аналитическим методом

3. КИНЕМАТИЧЕСКИЙ АНАЛИЗ

3.1. Определение крайних (мертвых) положений механизма

Для исследуемого механизма зубодолбежного станка крайними будут такие положения, когда кривошип и шатун то вытягиваются, то складываются  в одну линию. Тогда начальный и конечный углы определяются как:

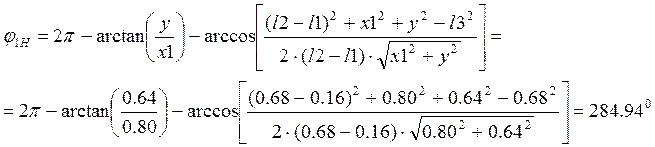
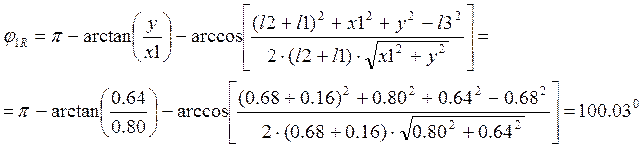
3.2. Построение планов положений исследуемого механизма

Выбираем масштабный коэффициент длин m_l =0,0032м/мм и рассчитываем чертежные размеры звеньев (табл. 3.1).

Таблица 3.1

Чертежные размеры звеньев

Планы механизма строим следующим образом:

-  отмечаем на чертеже неподвижные точки О и С и рисуем в них вращательные кинематические пары;

-  на расстоянии X₂ от точки С проводим траекторию движения ползуна 5;

-  проводим окружность радиусом ОА, которая является траекторией движения точки А, и дугу радиусом ВС, по которой движется точка В;

-  на траектории движения точки А отмечаем крайние положения А_н и А_к, которые соответствуют крайним положениям исследуемого механизма;

-  начиная от точки А₀ – начала рабочего хода ползуна, окружность радиуса ОА делим на 12 равных частей;

-  точки деления обозначаем через А₁, А₂, А₃ и т.д. в направлении вращения кривошипа

-  строим положения кривошипа, соединяя точки А_i с точкой О;

-  методом засечек строим план положений механизма для каждого положения кривошипа;

-  при построении планов механизма отмечаем положения центров масс звеньев 2 и 3 и строим их траектории.

3.3. Кинематическое исследование механизма

аналитическим методом

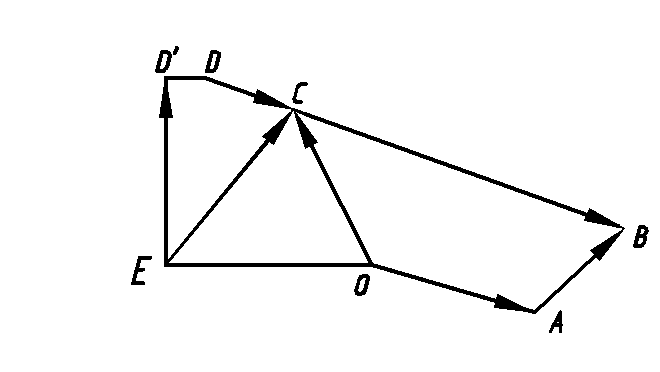
Структурную схему механизма располагаем в прямоугольной системе координат, начало которой помещаем в точку О. В соответствии с методом замкнутых векторных контуров со всеми звеньями механизма связываем векторы так, чтобы их последовательность образовала два замкнутых контура: ОАВСО и CDD^IEC (рис. 3.2). Углы, определяющие положения векторов, отсчитываем от положительного направления оси ОХ против хода часовой стрелки.

Рис. 3.2. Построение векторных контуров

Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора , причем все векторы, совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие – со знаком «-»:

                                             (3.1)

Уравнению (3.1) соответствуют два уравнения проекций на оси координат:

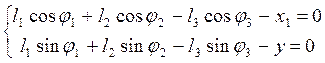                             (3.2)

Для упрощения нахождения углов j₂ и j₃ вместо одного сложного контура ОАВСО рассмотрим два простых ОАСО и АВСА. Для этого введем в рассмотрение вспомогательный вектор , соединяющий точки А и С механизма. При этом получим:

                                                 (3.3)

                                                 (3.4)

Представим уравнение (3.3) в проекциях на оси координат:

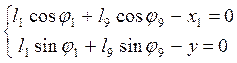                                     (3.5)

Откуда находим угол наклона вектора  для пятого положения

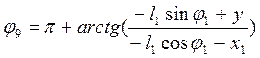                                        (3.6)

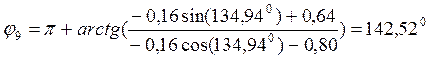
и его модуль

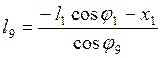                                                (3.7)

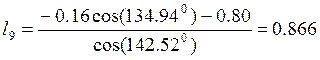
Углы j₂ и j₃ находим из уравнения (3.4), записав его в развернутом виде:

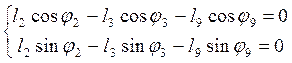                             (3.8)

Слагаемые, содержащие j₃, переносим в правые части уравнения, возводим оба уравнения в квадрат и складываем. После преобразования получим

откуда

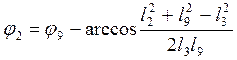                                         (3.9)

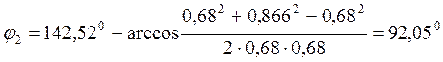
Для определения угла j₃ используем любое из уравнений (3.8). Например, из первого уравнения

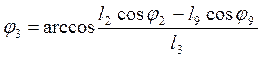                                      (3.10)

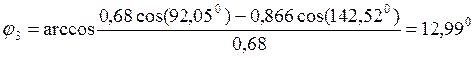
Уравнение замкнутости второго контура CDD^IEC имеет вид

                                                (3.11)

или в проекциях на оси координат

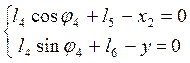                                              (3.12)

Учитывая, что j₄ = j₃ , из уравнений (3.12) находим вектора  и :

                                                   (3.13)

                                               (3.14)

Для нахождения положений точек S₂ и S₃ записываем уравнения замкнутости контуров OAS₂O  OS₃CO (рис. 3.2):

                                               (3.15)

                                               (3.16)

Из уравнений (3.15) и (3.16) находим координаты центров масс звеньев 2 и 3:

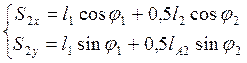                                      (3.17)

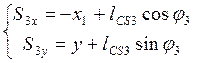                                          (3.18)

                                                  (3.19)

Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения для пятого положения приведены в табл. 3.2.

Таблица 3.2

Результаты расчета положений звеньев

Кинематические свойства механизма, когда закон движения начального звена еще не известен, найдем с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = 1 рад/с.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (3.2),(3.13) и (3.14). После дифференцирования уравнений (3.2) получим

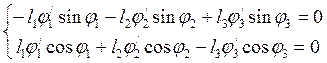                             (3.19)

где j₁^/ – аналог угловой скорости звена 1. Так как вращение первого звена происходит по часовой стрелке принимаем j₁^/ = -1; j₂^/, j₃^/ – аналоги угловых скоростей звеньев 2 и 3.

При дифференцировании уравнений (3.13) и (3.14) учитываем, что j₄^/ = j₃^/, а векторы Х₂ и У не зависят от обобщенной координаты, в итоге получаем

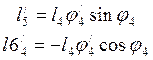                                   (3.20)