Подобие гидродинамических процессов
Несмотря на высокий уровень развития современной механики жидкости и вычислительной техники, существует достаточно большой класс задач, который может быть решен только экспериментальным путем. Заключительным этапом при создании современных гидравлических и газодинамических машин, приборов, летательных аппаратов, сооружений и т.д., является проведение экспериментальных исследований на модели или на натурном образце.
При постановке гидродинамического эксперимента необходимым инструментом является теория подобия, которая позволяет ответить на вопросы о том, по каким законам должна быть изготовлена модель испытуемого объекта и проведен пересчет опытных данных.
В теории подобия различают геометрическое подобие, являющееся подобием грани у областей течений, кинематическое подобие, под которым подразумевают подобие полей местной скорости, и динамическое подобие, являющееся подобием сил.
Геометрическое подобие.
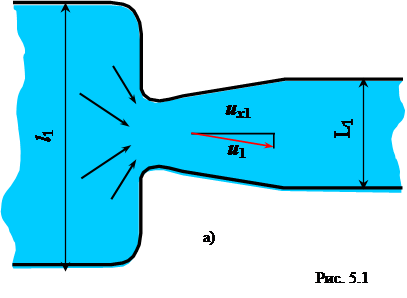
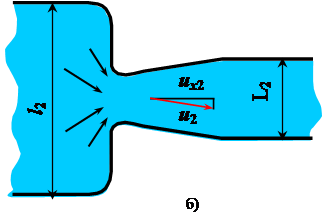
Рассмотрим в качестве примера натурный объект (рис. 5.1а) и его модель (рис. 5.1б).
 |
|||
 |
|||
Для получения области течения, геометрически подобного натуре, необходимо разделить все линейные размеры натуры на некоторое число ml = l1/l2, которое называется линейным масштабом, и полученные результаты приять за соответствующие линейные размеры модели.
Линейные размеры, связанные записанными выше соотношениями называют соответственными или сходственными. То же название носят точки, координаты которых удовлетворяют этому соотношению.
 Два
гидродинамических объекта будут геометрически подобными, если любой линейный
размер одного может быть получен из линейного размера другого путем умножения
на постоянный множитель.
Два
гидродинамических объекта будут геометрически подобными, если любой линейный
размер одного может быть получен из линейного размера другого путем умножения
на постоянный множитель.
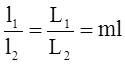 (5.1)
(5.1)
и 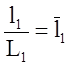 ;
; 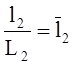 ;
; ![]() .
(5.2)
.
(5.2)
Следовательно, безразмерные координаты сходственных точек одинаковы.
Кинематическое подобие
Потоки 1 и 2 считаются кинематически подобными, если соотношение
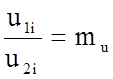 (5.3)
(5.3)
одинаково для любой пары сходственных точек, где u1, u2 - скорости в сходственных точках; u1i, u2i - их одноименные проекции на i-ю ось координат.
Если потоки неустановившиеся, то записанное выше условие выполняется в сходственные моменты времени
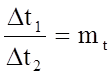 ,
(5.4)
,
(5.4)
где mt - масштаб времени, Dt1, Dt2 - интервалы времени, отсчитываемые от момента начала движения или иного условного начала отсчета времени.
Нетрудно убедиться, что кинематическое подобие потоков включает геометрическое подобие их линий тока. Уравнения линий тока для первого и второго потоков запишутся в виде
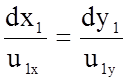 и
и 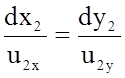 .
(5.5)
.
(5.5)
Выражая из этих соотношений dx1 и dx2, получаем
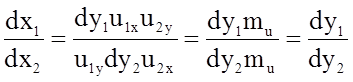 (5.6)
(5.6)
или 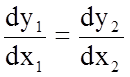 .
(5.7)
.
(5.7)
 Полученное соотношение показывает, что углы наклона
касательных к линиям тока в сходственных точках одинаковы для обоих потоков,
т.е. имеется геометрическое подобие линий тока. Для
установившихся потоков это будет одновременно и геометрическим подобием
траекторий жидких частиц.
Полученное соотношение показывает, что углы наклона
касательных к линиям тока в сходственных точках одинаковы для обоих потоков,
т.е. имеется геометрическое подобие линий тока. Для
установившихся потоков это будет одновременно и геометрическим подобием
траекторий жидких частиц.
Динамическое подобие
Динамически
подобными потоками называются такие потоки, у которых отношение 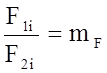 постоянно для любой пары сходственных
точек.
постоянно для любой пары сходственных
точек.
Под значениями F1i и F2i не обязательно подразумевать равно действующие силы, это могут быть и силы какой-либо определенной физической природы (тяжести, вязкости, упругости и др.). В этом случае мы будем иметь подобие данной категории сил.
Необходимо также отметить, что безразмерные значения сил в динамически подобных потоках одинаковы.
Подводя итог рассмотренному выше, можно утверждать, что кинематическое и динамическое подобие могут существовать только при наличии геометрического подобия. Вследствие этого, в дальнейшем мы будем рассматривать потоки в которых геометрическое подобие заведомо обеспечено.
Определим необходимые и достаточные условия, обеспечивающие механическое подобие.
Из определений кинематического и динамического подобия вытекает, что если эти подобия обеспечены, то безразмерные координаты сходственных точек, безразмерные скорости, безразмерные силы, безразмерные ускорения и плотности, т.е. все физические параметры механически подобных потоков в безразмерном виде одинаковы.
Физические параметры в любом из потоков связаны системой дифференциальных уравнений, описывающих движения. Так как в механически подобных потоках безразмерные значения физических параметров одинаковы, то и сами уравнения, представленные в безразмерном виде, должны быть одинаковы.
Совокупность параметров, определяющих какой-либо гидродинамический процесс, можно рассматривать как конкретное решение дифференциальных уравнений этого процесса. Решение дифференциальных уравнений осуществляется при вполне определенных значениях начальных и граничных условий. Таким образом, не только уравнение, но также безразмерные формы начальных и граничных условий в механически подобных потоках должны быть одинаковы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.