Подобие гидродинамических процессов и анализ размерностей, страница 3

q₁ = f(l₁, t₁, m₁, u₁ ..., n₁).                                        (5.14).

Величины q₁, l₁, ... n₁, выраженные в новых единицах L₁, T₁ и M₁, связаны с их значениями в старых единицах соотношениями

l₁ = a₁l;   t₁ = a_tt;   m₁ = a_mm

q₁ = ;   u₁ =, ...

 

Выражение (5.14) запишется в виде:

q= f(a_ll, a_mm, ,...).                  (5.15)

Принимая во внимание, что масштабы единиц измерения основных величин a_l, a_t и a_m произвольны, то в общем случае, их можно выбрать так, чтобы

;   ;   .

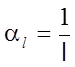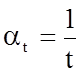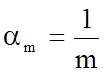При таком выборе масштабов мы, фактически, за единицы измерения принимаем основные величины l, t  и m, входящие в исходное уравнение. Тогда исходное уравнение (5.13) запишется в виде:

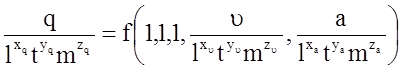.                            (5.16)

Входящие в это уравнение комплексы

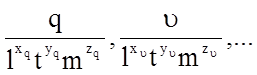
являются безразмерными параметрами.

Вводя для них соответствующие обозначения p_q, p_u, p_a ..., приходим к уравнению

p_q = f(1, 1, 1, p_u, p_a, ... p_p),                                        (5.17)

или к уравнению 

j (p_q, p_u, p_a, ... p_p) = 0.                                             (5.18)

Распространяя полученный результат на произвольное число величин, можно сформулировать, так называемую Пи- теорему:

Выражающая некоторый физический закон функциональная связь между n = k + S размерными величинами, из которых k величин имеют независимые размерности, может быть представлена в виде связи между n - k = S безразмерными комплексами p_q , p_u, ... p_p, каждый из которых является комбинацией из k + 1 размерных величин.

          Приведенное доказательство и формулировка p-теоремы имеют общефизический характер. С целью применения p-теоремы к задачам гидромеханики необходимо конкретизировать используемые величины и по возможности разделить их на группы. Составление списка величин облегчается в том случае, если процесс описан математически, в частности дифференциальными уравнениями, в противном случае необходимо четкое представление о физической сущности процесса, подкрепленное хорошо поставленным экспериментом.

В качестве параметров с независимыми размерностями в гидромеханике обычно выбирают следующие характерные величины: длину l, скорость u и плотность r, которые входят в каждую из безразмерных комбинаций p_i.

Определим безразмерные комбинации p_i для списка следующих параметров:

- l, a, b - линейные размеры,

-u - характерная скорость, 

-r - плотность жидкости;

-Dр - перепад давления,

-t - касательное напряжение,

- g - ускорение свободного падения,

-m - вязкость;

-s - поверхностное натяжение;

-e - упругость жидкости.

Таким образом, общее количество параметров n = 11, параметров с независимыми размерностями k = 3, безразмерных комплексов - 8. Согласно общей формуле

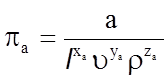.                                              (5.19)

Поскольку p_абезразмерная величина, то, очевидно, должно быть: x_a = 1; y_a = 0; z_a = 0.

Следовательно,

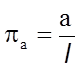.                                                (5.20)

Аналогично

p_b = b/l.                                               (5.21)

Далее, для p_p имеем

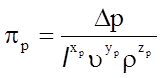    .                                          (5.22)

Значение x_p, y_p и z_p определяется из сравнения размерности левой и правой частей записанного уравнения.

Принимая во внимание, что

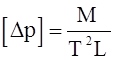; [ l ] = L; [ u ] = L/T; [ r ] = M/L³, то

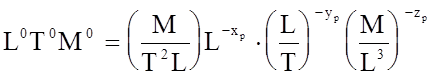.                          (5.23)

Приравнивая показатели степени при одноименных величинах в левой и правой частях, получим: