Подобие гидродинамических процессов и анализ размерностей, страница 2

Выбирая в качестве характерных значений физических параметров L, V, T, P, F₀ получаем следующие значения безразмерных параметров

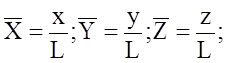                                               (5.8)

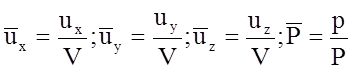;                                      (5.9)

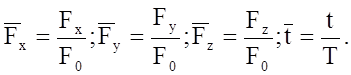                                     (5.10)

Плотность и вязкость принимаем постоянными величинами и, следовательно, отсутствует необходимость приведения их к безразмерному виду.

С учетом принятых безразмерных параметров, уравнения Навье - Стокса запишутся в виде (записываем только первое уравнение)

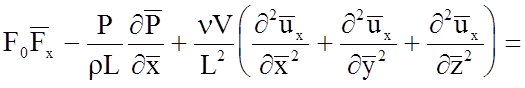
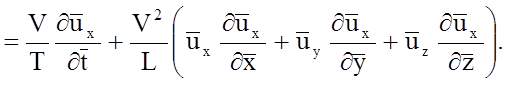             (5.11)

Разделим все члены этого уравнения на коэффициент при конвективном ускорении V²/L и получим выражение

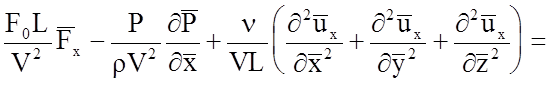
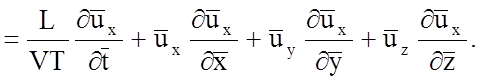,                      (5.12)

в котором все члены уравнения, включая комплексы, составленные из характерных параметров, являются безразмерными величинами.

Входящие в полученное выражение безразмерные комплексы играют роль критериев подобия:

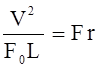 -  число Фруда (характеризует отношение силы инерции к силе тяжести).

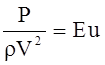 - число Эйлера (отношение силы давления к силе инерции).

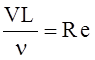 - число Рейнольдса (отношение силы инерции к силе вязкости).

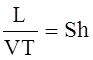 - число Струхаля (отношение локальной инерционной силы к конвективной).

Для механически подобных потоков необходимо Fr = idem; Eu = idem; Re = idem; Sh = idem.

Таким образом, одинаковые безразмерные дифференциальные уравнения, описывающие группу гидродинамических процессов, вместе с безразмерными условиями однозначности (начальными и граничными условиями), а также одинаковые значения критериев подобия являются необходимыми и достаточными условиями механического подобия.

Необходимо отметить, что обеспечить постоянство всех критериев подобия одновременно для большинства рассматриваемых случаев невозможно. Вследствие этого, необходимо в каждом гидродинамическом явлении указать лишь одну силу, влияние которой на характер движения является основным, определяющим. Тогда, игнорируя другую силу, можно моделировать лишь по одному критерию.

Практикой исследований установлено, что для течения со свободной поверхностью в поле силы тяжести лучше использовать критерий Фруда, а для напорных течений в закрытых трубах и каналах - критерий Рейнольдса. Уравнения и зависимости, связывающие параметры гидродинамических процессов, выражают определенные физические законы, и они не зависят от системы единиц измерения.

Представляется целесообразным определить такие комбинации физических параметров, отыскание связей между которыми дает результаты, относящиеся сразу к целому классу явлений.

          Рассмотрим зависимость

q = f(l, t, m, u, r, ... P),                                          (5.13)

которая выражает связь между размерной величиной q и размерными независящими одна от другой величинами l, t, m.

Допустим, что из числа записанных величин l, t, m, u, r ... P, первые три, т.е. l, t и m имеют независимые размерности. Тогда размерности остальных величин можно выразить через эти размерности l, t и m. В том случае, если L, T и М соответственно единицы измерения для l, t и m, то формулами размерности будут

[ l ] = L;   [ t ] = T;   [ m ] = M;

[ u ] =  ; [ a ] =  .

Изменим теперь единицы измерения основных величин соответственно в a_l, a_t и a_m раз, т.е. перейдем к единицам

L₁ = a₁L;   T₁ = a_tT;   M₁ = a_mM.

Тогда величины q, l, t, m, u, a ... будут выражаться в новых единицах, но вид уравнения не должен измениться, т.к. физический закон не зависит от выбора системы единиц. В новых единицах рассматриваемая зависимость запишется в виде