Подобие гидродинамических процессов и анализ размерностей, страница 4

- 1 - x_p - y_p + 3z_p = 0;                                              (5.24)

- 2 + y_p = 0;                                                   (5.25)

    1 - z_p = 0.                                                   (5.26)

Решая эту систему, находим, что x_p = 0; y_p = 2; z_p = 1 и, подставляя эти значения в (5.22), получаем

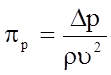.                                                 (5.27)

Аналогичным способом находим остальные безразмерные комплексы:

;    ;    ;    ;    .

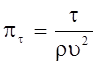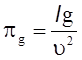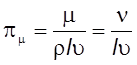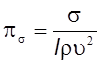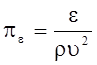Безразмерные параметры p_а и p_b характеризуют геометрию потока; p_р ‑ известное число Эйлера Е_u, p_t - безразмерное напряжение, обусловленное силами трения. Величины 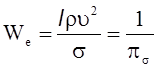и 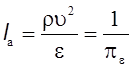носят название соответственно числами Вебера и Коши, которые соответственно характеризуют действие сил поверхностного натяжения и упругости. Безразмерные параметры  и представляют собой соответственно числа Фруда и Рейнольдса. Полученный результат можно представить в одной из форм:

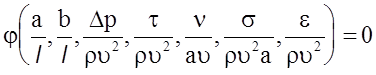                                (5.28)

или 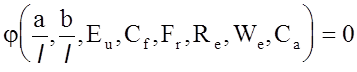    ,                                  (5.29)

где C_f = 2p_t.

          Любой из перечисленных параметров этих функций может рассматриваться как зависимый, а остальные как аргументы. В большинстве случаев искомыми величинами являются Е_u или С_f.

Необходимо отметить, что метод размерностей не позволяет установить в конкретных случаях вид функции j, однако позволяет сократить число переменных и рационально спланировать эксперимент.

В качестве примера использования метода размерностей рассмотрим сопротивление движению несжимаемой жидкости в цилиндрических трубах.

Определим структуру зависимости падения давления Dр на участке длиной l круглой гладкой цилиндрической трубы. Считаем известным, что при движении жидкости с известными параметрами r и m по трубе фиксированного диаметра устанавливается однозначное соответствие между характерной скоростью и падением давления Dр на заданном участке l.

При этом устанавливается и определенное значение касательного напряжения t, величина которого вполне определяется значением Dр и поэтому не может служить независимым параметром.

С учетом данных соображений в список параметров, определяющих явления, включим величины l, d, u, r, Dp, m.

Исходя из изложенного выше, шесть параметров мы можем сократить всего до трех p-параметров:

.

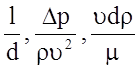Вследствие этого, искомая функция должна принять вид:

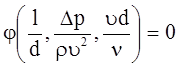,                                                (5.30)

или, принимая за искомую функцию выражение , получаем зависимость от двух безразмерных параметров:

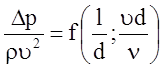.                                                   (5.30а)

Экспериментально установлено, что между величинами Dр и l существует линейная зависимость. Поэтому выражение (5.30а) можно преобразовать к виду

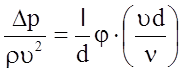.                                                   (5.31)

Вводя обозначение l = 2 j, получаем

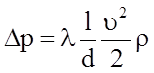     ,                                                   (5.32)

где l = l(Re), а 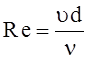- число Рейнольдса.

Данная формула была впервые получена эмпирическим путем и является основной расчетной формулой для определения потерь давления. Для гидравлических гладких труб  l = l(Re), для шероховатых труб  l = f (Re, Dd) где D - средняя высота выступов. Параметры l/d и D/d обеспечивают геометрическое подобие потоков в трубах разных диаметров, длин и шероховатостей и имеют одинаковое значение для всех геометрически подобных труб. Механическое подобие таких потоков обеспечивается геометрическим подобием и критерием Рейнольдса.