Уравнение Бернулли для элементарной струйки несжимаемой жидкости. Энергетическая интерпретация уравнения Бернулли

расстояния до центров тяжести объема а и b от некоторой горизонтальной плоскости.

С точностью до малых порядков можно считать, что z₁ и z₂ - ординаты центров сечений I и II.

Работа сил давления на боковую поверхность выделенного объема равняется нулю, т.к. эти силы нормальны к этой поверхности.

Работа сил давления на торцы равна разности

p₁ dw₁ u₁ dt - p₂ dw₂ u₂ dt.                                      (4.7)

Таким образом, изменение кинетической энергии запишется в следующем виде

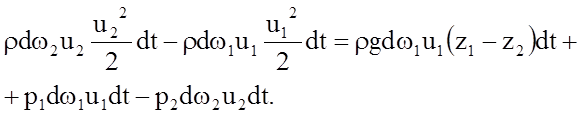         (4.8)

Разделив на dt и сгруппировав члены этого уравнения, получаем:

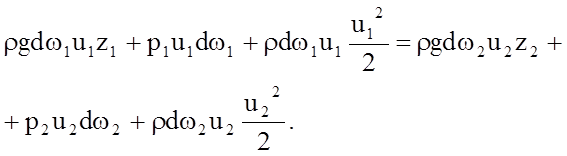          (4.9)

Заменив u₁dw₁ = u₂dw₂ = dQ, и разделив затем левую и правую части этого уравнения на величину r·g·dQ, получим

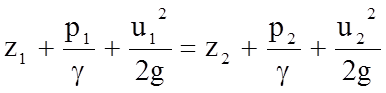.                              (4.10)

Полученное уравнение и носит название уравнение Бернулли, написанное для участка элементарной струйки между сечениями I и II.

Его можно представить также в разностной форме

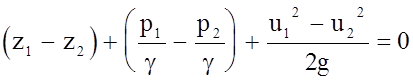,                       (4.11)

или в приращениях: 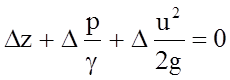.                                                        (4.12)

Переходя к дифференциальному виду, имеем

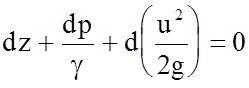.                                    (4.13)

Принимая во внимание, что сечения I и II взяты произвольно, имеем

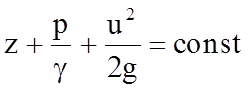.                                      (4.14)

Геометрическая интерпретация уравнения Бернулли.

Отнесем струйку к системе координат xyz и напишем уравнение Бернулли для трех произвольных сечений струйки:

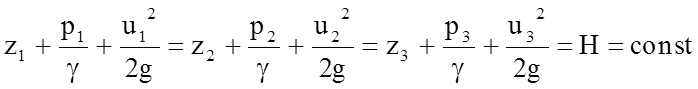.           (4.15)

Здесь:

·    z - геометрическая высота центра тяжести сечения над плоскостью xoy.

·    - пьезометрическая высота

·    - скоростная высота или скоростной напор.

Все эти величины имеют нелинейную размерность.

Величину Н называют полным напором в данном сечении струйки.

Для каждого поперечного сечения элементарной струйки величина Н может быть представлена совокупностью отрезков z,  и . Соединив между собой концы отрезков Н, получим кривую, расположенную в горизонтальной плоскости. Эту плоскость и кривую на ней называют плоскостью и линией полного напора.

Соединив кривой концы отрезков , получим линию, которую называют пьезометрической линией или пьезометрической кривой.

По длине струйки меняются слагаемые уравнения Бернулли. Если сечение расширяется и, следовательно, скорость уменьшается, то уменьшается скоростной напор, но возрастает сумма (z + ).

Энергетическая интерпретация уравнения Бернулли.

Если рассматривать уравнение Бернулли как уравнение энергии, то каждое слагаемое этого уравнения надо расценивать как некоторую составляющую полной энергии (потенциальную или кинетическую), и каждое из этих слагаемых должно измеряться в единицах работы.

Уравнение Бернулли представлено в линейных единицах, поэтому, чтобы перевести его в уравнение работы, необходимо помножить его на единицу силы (1Н). В результате получим Дж = Н×м и, следовательно, уравнение представляет собой некоторую энергию, отнесенную к 1Н жидкости, проходящей через данное сечение в 1с. Такую энергию называют удельной.

В соответствии с этим z будет удельной потенциальной энергией, обусловленной тем, что данный 1Н жидкости находится на высоте z  и может совершить работу, равную z дж.

Аналогично  будет удельной потенциальной энергией давления.

Величина  представляет собой удельную кинетическую энергию.

Пьезометрическая линия отделяет область изменения потенциальной энергии от области изменения кинетической энергии. Легко видеть, что с энергетической точки зрения уравнение Бернулли показывает, что сумма потенциальной энергии (положение и давление) и кинетической энергии есть величина постоянная