Определение статистической оценки математического ожидания и дисперсии

Выборка 1

Выборка 2

Выборки случайных чисел распределены по нормальным законам

1.Определение статистической оценки математического ожидания и дисперсии

Точечная оценка математического ожидания

Точечная оценка дисперсии

Среднее квадратическое отклонение

2. Проверка провдоподобия гипотезы о принадлежности двух выборок единой генеральной совокупности.

2.1 Порядковый критерий Вилконсона

Нулевая гипотеза состоит в том, что при всех значениях аргумента функции распределения равны между собой:

F1(x)=F2(x)

Располагаем варианты обеих выборок в возрастающем порядке, т.е. в виде одного вариационного ряда:

Находим наблюдаемое значение критерия - сумма порядковых номеров вариант первой выборки, при этом перенумеровываем выборки так, чтобы n1<n2:

Находим нижнюю критическую точку по таблице приложения 10, где w ниж кр является функцией Q=a/2 (a=0,05), n1 и n2:

Находим верхнюю критическую точку:

Оснований отвергнуть гипотезу нет, так как w ниж кр < W набл < w верх кр, следовательно по данному критерию две выборки принадлежат одной генеральной совокупности.

2.2 Критерий Фишера-Снедекора (равенства генеральных дисперсий)

Нулвевая гипотеза: D(X)=D(Y)

Конкурирующая гипотеза:

Наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей):

Находим критическую точку F кр по таблице критических точек распределения ФишераСнедекора при a=0.05:

Число степеней свободы большей дисперсии:

Число степей свободы меньшей дисперсии:

Оснований отвергнуть нулевую гипотезу нет, так как F набл < F кр, следовательно, D(X)=D(Y), а значит выборки принадлежат одной генеральной совокупности.

2.3 Критерий Стьюдента (сравнения средних)

Нулевая гипотеза: M(X)=M(Y)

Конкурирущая гипотеза:

Число степеней свободы:

По таблице критических точек распределения Стьюдента, по заданному уровню значимости a=0,05 и числу степеней свободы определяем критическую точку

t двуст.кр :

Оснований отвергнуть нулевую гипотезу нет, так как

Следовательно, M(X)=M(Y)

3. Объединение двух выборок и определение точечных оценок математического

ожидания и дисперсии для объединенной выборки

Так как гипотеза о принадлежности двух выборок единой генеральной совокупности не противоречит располагаемому статистическому материалу, то выборки можно объединить.

Точечная оценка математического ожидания

Точечная оценка дисперсии

Среднее квадратическое отклонение

4. Интервальные оценки объединенной выборки

Доверительная вероятность:

4.1 Интервальная оценка для статистической оценки математического ожидания при неизвестном s

t - квантиль распределения Стьюдента при óðîâíå значимости a=0,05 и числе степеней свободы n3-1=29

4.1 Интервальная оценка для статистической оценки дисперсии

Квантиль распределения для уровня значимости a/2=0,025 и числа степеней свободы n3-1=29:

Квантиль распределения для уровня значимости 1-a/2=0,975 и числа степеней свободы n3-1=29:

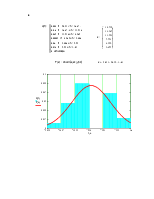
5. Проверка гипотезы о нормальности закона распределения объединенной

выборки по критерию Пирсона

Число интервалов

Для уровня значимости a=0,05 и числа степеней свободы к=s-3, где s - число частичных интервалов, к=3

Следовательно, оснований отвергнуть нулевую гипотезу нет, объединенная выборка распределена по нормальному закону.

6.

7. Cистема двух случайных величин. Оценки математического ожидания и дисперсии.

Оценка коэффициента корреляции между двумя случайными величинами.

Точечная оценка математического ожидания

Точечная оценка дисперсии

Среднее квадратическое отклонение

Выборочный коэффициет корреляции

8. Проверка гипотезы о значимости выборочного коэффициента корреляции

Нулевая гипотеза: о равенстве генерального коэффициента корреляции нулю rг=0

Конкурирующая гипотеза:

Уровень значимости: a=0,05

Наблюдаемое значение критерия:

Из  таблицы критических точек распределения Стьюдента для числа степеней свободы

k=n-2=13 и уровня значимости a=0,025:

Нулевая гипотеза о равенстве генерального коэффицинта корреляции нулю приминается, так как Тнабл < tкр. Равенство генерального коэффициента нулю означает, что X и Y некоррелированы и выборочный коэффициент корреляции незначим.

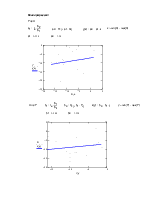
Линии регрессии:

Y на X

X на Y