Министерство образования и науки Российской Федерации
Новосибирский Государственный Технический Университет

Кафедра техники и электрофизики высоких напряжений
Расчётно-графическая работа
по курсу: «Теория вероятностей и математическая статистика»
ВАРИАНТ № 7
ФЭН Группа: ЭнБ-81
Студент: Пасевич Е.Б.
Проверил: Шальнев В.Г.
Задание на работу:
Заданы выборки случайных величин X* и Y*:
X*
-2.369 0.4445 -3.494 1.736 -4.375 9.5 -13.63 4.351 10.9 5.425
5.878 -4.857 -7.879 2.32 7.372 5.827 -3.817 2.547 2.48 -4.012
Y*
-3.135 -2.767 -1.73 -2.322 1.255 -1.867 -1.366 6.448 0.9704 10.43
Оценки математических ожиданий и дисперсий генеральных совокупностей величин X и Y могут быть определены по выражениям (1.1) и (1.2) соответственно.
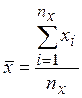 , (1.1)
, (1.1)
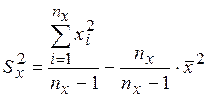 , (1.2)
, (1.2)
где ![]() - объём выборки из генеральной
совокупности X.
- объём выборки из генеральной
совокупности X.
В нашем случае числовые характеристики принимают следующие значения:
![]() ;
; ![]() ;
;![]()
![]() ;
;![]() ;
;![]()
2.1. Порядковый критерий Вилькоксона.
В дальнейшем, гипотезу о принадлежности двух выборок единой генеральной совокупности будем называть нулевой гипотезой.
Порядковый критерий Вилькоксона основан на определении степени «перемешанности» единого вариационного ряда для двух выборок.
Алгоритм расчёта уровня статистической значимости нулевой гипотезы c помощью порядкового критерия Вилькоксона:
x x x x x x x y y x
-13.66 -7.879 -4.857 -4.375 -4.012 -3.815 -3.494 -3.135 -2.767 -2.369
y y y y x y y x x x
-2.322 -1.867 -1.73 -1.366 0.445 0.9704 1.255 1.736 2.32 2.48
x x x x x y x x y x
2.547 4.351 5.425 5.827 5.878 6.448 7.372 9.5 10.43 10.9
Определяем числа инверсий
![]() ,
, ![]() .
.
Проверка: И X–Y + И Y–X = 400; И X–Y + И Y–X = nX · nY = 400.
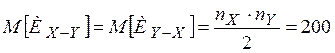 , (2.1)
, (2.1)
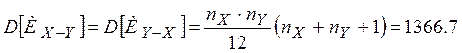 , (2.1)
, (2.1)
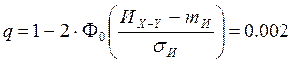 . (2.3)
. (2.3)
2.2. Критерий равенства математических ожиданий.
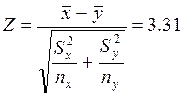 . (2.4)
. (2.4)
Случайная величина Z (распределена по нормальному закону с нулевым математическим ожиданием и единичной дисперсией. Тогда:
![]() . (2.5)
. (2.5)
2.3. Критерий равенства дисперсий (критерий Р. Фишера).
В нашем случае SY<SX, поэтому критерий равенства дисперсий (критерий Р. Фишера) принимает следующий вид
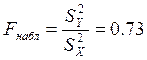 . (2.6)
. (2.6)
Уровень значимости нулевой гипотезы определяем так
![]() . (2.7)
. (2.7)
Вывод по пунктам 2.1, 2.2 и 2.3
Гипотеза о принадлежности выборок X и Y единой генеральной совокупности противоречит располагаемому статистическому материалу с уровнями значимости:
· По критерию Вилькоксона – q=0.002
· По критерию равенства математических ожиданий (критерий Z) – q=0.001,
Не противоречит:
· По критерию равенства дисперсий (критерий F) – q=0.5
131.7 136.7 139.4 141.0 141.2 144.1 145.9 146.8
147.6 148.9 149.3 150.3 150.5 152.0 153.2 153.4
153.8 155.0 155.6 156.5 157.4 157.6 158.0 158.6
158.7 159.4 161.0 161.8 162.2 163.3 163.8 164.9
165.4 166.3 168.2 171.3 173.3 176.0 181.2 184.1
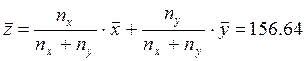 (3.1)
(3.1)
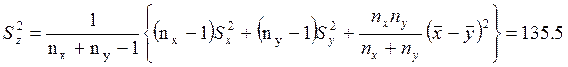
![]()
С вероятностью 0.95
математическое ожидание единой генеральной совокупности Z
принадлежит интервалу 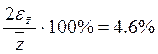 .
.
С вероятностью 0.95 дисперсия единой генеральной
совокупности Z принадлежит интервалу 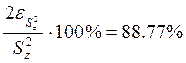 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.