Проверка правдоподобия гипотезы о принадлежности заданных выборок единой генеральной совокупности, страница 2

5.1. Критерий Пирсона (критерий – χ²).

Разбиваем весь диапазон объединённой выборки Z на 6 интервалов/

Результаты предварительных вычислений при применении критерия Пирсона представлены в таблице 5.1

Таблица 5.1

Предварительные вычисления при применении критерия Пирсона

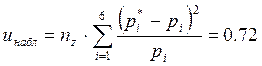                                          (5.1)

При этом уровень значимости по критерию Пирсона

.                                             (5.2)

5.2. Критерий Мизеса (nω²).

Критерий  Мизеса о нормальности закона распределения СВ Z записывается в виде:

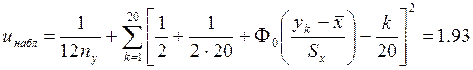.                      (5.3)

Найденному значению и_набл соответствует уровень значимости по критерию Мизеса,     равный q = 0.0002.

Следовательно, гипотеза о нормальности закона распределения единой генеральной совокупности Z не противоречит располагаемому статистическому материалу с уровнями значимости::

·  По критерию Пирсона – q=0.88,

Противоречит располагаемому статистическому материалу:

·  По критерию Мизеса – q=0.0002

Гистограмма по данным выборки Z^* и гипотетическая плотность распределения Z представлены на рис.5.1

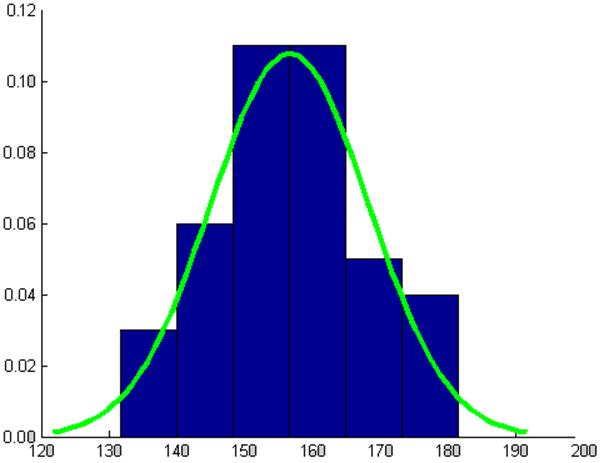
Рис. 5.1 Гистограмма по данным выборки Z^* и гипотетическая плотность распределения Z

6. Определение статистических оценок корреляционного момента K_xy (K^*_xy) и коэффициента корреляции r_xy (ρ_xy).

Для решения этой задачи составим корреляционную таблицу (табл. 6.1), при этом обе выборки (X^* и Y^*) разобьём, например, на 4 интервала.

Таблица 6.1

Корреляционная таблица

Числовые характеристики , , ,  определим по следующим выражениям:

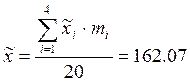,                                                                   (6.1)

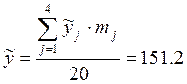,                                                                    (6.2)

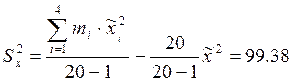                  ,                                               (6.3)

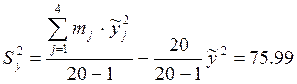.                                         (6.4)

Статистическую оценку корреляционного момента определим как

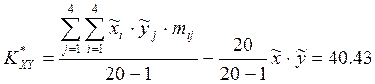.                  (6.5)

Тогда статистическая оценка коэффициента корреляции равна

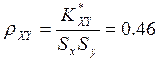.                                                  (6.5)

Проверка гипотезы об отсутствии корреляционной связи между            величинами X и Y.

Для оценки правдоподобия гипотезы об отсутствии корреляционной связи воспользуемся Т-статистикой Стьюдента:

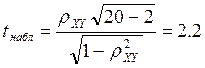.                                         (7.1)

При этом

.                                                (7.2)

Следовательно, гипотеза об отсутствии корреляционной связи между случайными величинами X и Y  противоречит располагаемому статистическому материалу с уровнем значимости 0.03.

Определение доверительного интервала для оценки коэффициента корреляции:

С вероятностью 0.95 коэффициент корреляции принадлежит интервалу

.

7. Определение коэффициентов линейной регрессии Y^* на X^* и оценка их статистической значимости.

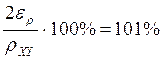Коэффициенты линейной регрессии Y^* на X^* найдём с помощью метода наименьших квадратов. В соответствии с этим методом, если , то коэффициенты b₀ и b₁ могут быть определены по следующим выражениям

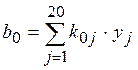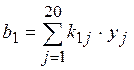,                                                   (9.1)

где

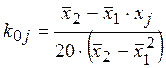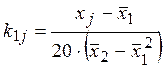,             ,                         (9.2)

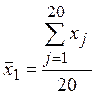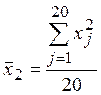,               .                                                  (9.3)

В итоге получаем следующие значения для коэффициентов линейной регрессии:

, .

Уравнение линейной регрессии Y^* на X^* принимает следующий вид (рис. 9.1):

.

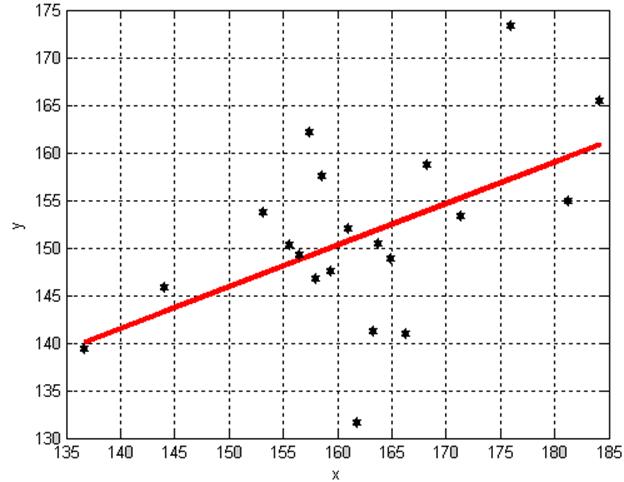
Рис. 9.1 Линейная регрессия

Проверим статистическую значимость полученной линейной регрессии по критерию Фишера.

 (получено ранее),

,

,

.

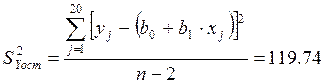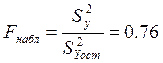Следовательно, гипотеза о линейности регрессии Y на X не противоречит располагаемому статистическому материалу с уровнем значимости q=0.6 по критерию Фишера.