Вычисление определенного интеграла. Построение трехточечной интерполяционной формулы прямоугольника, трапеции, квадратурных формул Симпсона и Ньютона-Котеса максимально возможной алгебраической степени точности

Санкт-Петербургский Государственный Университет

Факультет Прикладной Математики – Процессов Управления

Вычисление определенного интеграла

Выполнил: Шупило Александр

Группа: 314

2008 г.

Цель задания:

Убедиться в необходимости использования квадратурных формул для вычисления «неберущихся» определенных интегралов. Построить квадратурные формулы, используя правило прямоугольников средней точки, формулу трапеции, правило парабол (квадратурная формула Симпсона), квадратурные формулы Ньютона – Котеса. Научиться управлять численным процессом с целью обеспечения заданной точности

Содержание задания:

1. Построить трехточечную интерполяционную формулу прямоугольника, трапеции, Симпсона и Ньютона – Котеса максимально возможной алгебраической степени точности.

Оценить методическую погрешность. На базе построенной интерполяционной квадратурной формулы построить составную  и, увеличивая число разбиений на частичные отрезки и оценивая ее остаточный член по Ричардсону, добиться заданной точности.

Решение задачи

1.Рассматриваем функцию

на интервале [a, b], где a=3,5, b=3,7.

2.Построим квадратурную формулу прямоугольника максимально возможной алгебраической степени точности, добиваясь оценки погрешности (по правилу Рунге) 10^(-6).

Получаем:

Значение интеграла: −593.088873010700826408913259284

Число шагов: 81920

2.Построим квадратурную формулу трапеции максимально возможной алгебраической степени точности, добиваясь оценки погрешности (по правилу Рунге) 10^(-6).

Получаем:

Значение интеграла: −593.088873301272838908007888187

Число шагов: 163840

3.Построим квадратурную формулу Симпсона максимально возможной алгебраической степени точности, добиваясь оценки погрешности (по правилу Рунге) 10^(-6).

Получаем:

Значение интеграла: −593.088873182687578473505020987

Число шагов: 640

Весовая функция :

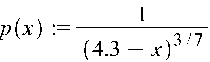
4.Построим составную квадратурную формулу Ньютона – Котеса с весовой функцией р(х) максимально возможной алгебраической степени точности. Оценка погрешности равна 10^(-6).

Получаем:

Значение интеграла: −3246.87592630977302651989810631

Число шагов: 2560