Санкт-Петербургский государственный университет
Решение систем уравнений методом Ньютона
Выполнил: Слупко Егор Алексеевич
Группа: 316
Вариант: 15
1. Локализовать решение системы уравнений
sin(y+0.5)-x=1
y+cos(x-2)=0
2. Реализовать метод Ньютона для систем уравнений на языке С++ и с его помощью получить решение этой системы с точностью до 0.0001.
Локализацию корня проведем графически. Построим кривые, соответствующие уравнениям системы:
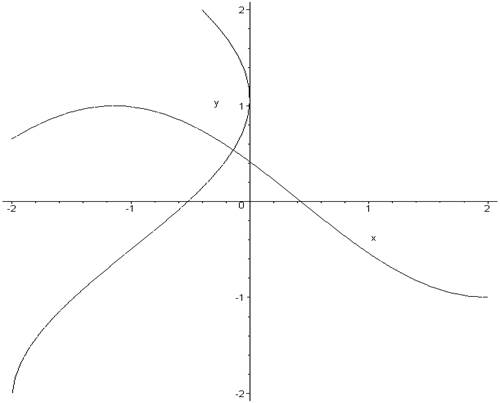
Система имеет одно решение. Примем за начальное приближение X0=(0,0.8)T.
#include <iostream>
#include <math.h>
class vect
{
private:
double x1,x2;
public:
double GetX1() {return x1;}
double GetX2(){return x2;}\
void SetV(double a, double b) {x1=a; x2=b;}
};
struct Matr
{
double x11,x12,x21,x22;
};
vect Razn(vect a, vect b)
{
vect c;
c.SetV(a.GetX1()-b.GetX1(), a.GetX2()-b.GetX2());
return c;
}
vect Mult(Matr A, vect b)
{
vect c;
c.SetV(A.x11*b.GetX1()+A.x12*b.GetX2(),A.x21*b.GetX1()+A.x22*b.GetX2());
return c;
}
double abs(vect a)
{
return sqrt(a.GetX1()*a.GetX1()+a.GetX2()*a.GetX2());
}
int main()
{
double x,y;
std::cout<<"Введите начальные х и у:\n x = ";
std::cin>>x;
std::cout<<" y = ";
std::cin>>y;
double eps=1,E;
std::cout<<"Введите степень точности:\n Е = ";
std::cin>>E;
vect F, X;
X.SetV(x,y);
int i =1;
for(; eps>E; i++)
{
F.SetV(sin(X.GetX2()+0.5)-X.GetX1()-1,X.GetX2()+cos(X.GetX1()-2));
vect FF;
Matr dF;
double less = -1 + cos(X.GetX2()+0.5) * sin(X.GetX1()-2);
dF.x11 = 1/less;
dF.x12 = -cos(X.GetX2()+0.5)/less;
dF.x21 = sin(X.GetX1()-2)/less;
dF.x22 = -1/less;
FF = Mult(dF,F);
vect R = X;
X = Razn(X,FF);
eps = abs(Razn(X,R));
}
std::cout<<"Результаты:\n х=("<<X.GetX1()<<";"<<X.GetX2()<<")\n";
std::cout<<"Количество итераций "<<i<<std::endl;
return 0;
}
Система уравнений задана в коде программы статично. Значения начального приближения и степени точности вводятся по запросу программы, что дает возможность провести серию тестов, показывающих зависимость числа итераций от степени точности и начального приближения.
По завершении работы программа выводит следующие результаты:
Введите начальные х и у:
x = 0
y = 0.8
Введите степень точности:
Е = 0.0001
Результаты:
х=(-0.138685;0.537853)
Количество итераций 5
Установим зависимость числа итераций от велечины начального приближения и степени точности:
|
x0 |
y0 |
E |
Итерации |
|
0 |
0.8 |
0.0001 |
5 |
|
-1 |
0 |
0.0001 |
6 |
|
2 |
0.8 |
0.0001 |
6 |
|
0 |
2 |
0.0001 |
9 |
|
0 |
0.8 |
0.0000001 |
5 |
Из таблицы видно, что наибольшее изменение числа итераций дает отдаление начального приближения от корня по оси OY, в то время как изменение степени точностив 1000 раз не меняет число итераций вовсе. Очевидно, это вызвано довольно спокойным поведением функции в окрестности корня.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.