Равномерное разбиение интервала интегрирования. Вычисление интеграла с помощью квадратурной формулы Гаусса

> restart;// Задание исходных параметров,нашей функции,весовой функции,их графики,вычисление интеграла

> a := 1.7;

b := 3.2;

 alfa := 0;

 beta:=1/4;

f:=(x)->3*cos(0.5*x)*exp(x/4)+5*sin(2.5*x)*exp(-x/3)+2*x;

p:=(x)->((x-1.7)^0)*((3.2-x)^(1/4));

int(f(x)*p(x),x=1.7..3.2);

> n:=1000;// Вычисление интеграла по формуле (3) (равномерное разбиение интервала интегрирования)

integral:=proc(n) local i,h,R,F,k;

F[0]:=0;

h:=abs(b-a)/n;

for i from 1 by 1 to n do

k[i]:=a+(i-1/2)*h;

F[i]:=F[i-1]+f(k[i])*p(k[i]);

end do;

R:=h*F[i-1];

return R;

end proc;

evalf(integral(n),10);

> restart; Вычисление интеграла с помощью квадратурной формулы Гаусса

_MG:=proc(n,a,b)::real; //вычисление моментов

global MG;

local i,p;

p:=(x)->((x-1.7)^0)*((3.2-x)^(1/4));

for i from 0 by 1 to 2*n+1 do

MG[i]:=int(p(x)*x^i,x=a..b);

 (evalf(MG[i]));

end do;

end proc;

> with(LinearAlgebra)://решение СЛАУ для нахлждения коэффициентов а[i]

_a_G:=proc(n)

global a_G;

local MG1_G,MG2_G,i,s;

a_G:=Matrix(n+1,1):

MG1_G:=Matrix(n+1,n+1):

MG2_G:=Matrix(n+1,1):

for i from 1 by 1 to n+1 do

MG2_G[i,1]:=(-1)*MG[n+i]:

end do:

for s from 0 by 1 to n do

 for i from 1 by 1 to n+1 do

  MG1_G[i,s+1]:=MG[i-1+s];

 end do:

end do:

a_G:=LinearSolve(MG1_G,MG2_G);

return (evalf(a_G));

end proc;

> W_G:=proc(x,n) //составляем полином w(x)

local R,i;

R:=x^(n+1);

for i from 0 by 1 to n do

R:=R+evalf(a_G[1+i,1]*x^i);

end do;

return R;

end proc;

> solve_w_G:=proc(x,n) //находим корни w(x)

global v;

v:=solve(W_G(x,n));

return v;

end proc;

> with(LinearAlgebra): //находимкоэф. A[i]

_A_G:=proc(n)

global A_G;

local s,i,Solve_G,Mu_G;

Solve_G:=Matrix(n+1,n+1):

A_G:=Matrix(n+1,1):

Mu_G:=Matrix(n+1,1):

for s from 0 by 1 to n do

 for i from 1 by 1 to n+1 do

  Solve_G[s+1,i]:=v[i]^s;

 end do:

end do:

for s from 0 by 1 to n do

Mu_G[s+1,1]:=MG[s];

end do:

A_G:=LinearSolve(Solve_G,Mu_G);

(evalf(A_G));

end proc;

> _integral_G:=proc(n) //объединяем все в 1 процедуру для нахождения интеграла

local integral_G,i,f;

integral_G:=0;

f:=(x)->3*cos(0.5*x)*exp(x/4)+5*sin(2.5*x)*exp(-x/3)+2*x;

for i from 1 by 1 to n+1 do

integral_G:=A_G[i,1]*f(v[i])+integral_G:

end do:

return evalf(integral_G);

end proc;

> a:=1.7;

b:=3.2;

n:=2;

_MG(n,a,b):

> _a_G(n);

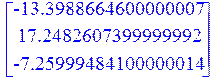
> W_G(x,n);

> solve_w_G(x,n);

> _A_G(n);

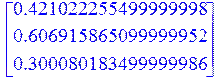
> _integral_G(n);

> n:=3; Погрешность

f:=(x)->3*cos(0.5*x)*exp(x/4)+5*sin(2.5*x)*exp(-x/3)+2*x;

p:=(x)->((x-a)^0)*((b-x)^(1/4));

with(Optimization):

M:=Maximize(diff(f(x),x$(2*n)),x=1.7..3.2);

M[1]*int(abs(p(x)*(W_G(x,n-1))^2),x=1.8..2.9)/(2*n)!;

Реализуем составную формулу:

> a:=1.7;

b:=3.2;

m:=2;

   

H0:=(b-a)/3;//разбивам интервал на отрезки

n:=3;

interval:=proc(a,b)

global a_interval;

local i,j;

j:=1;

i:=a;

a_interval[0]:=a;

while (i<b) do

 a_interval[j]:=a_interval[j-1]+H0;

 i:=i+H0;

 print(a_interval[j-1],a_interval[j]);

 j:=j+1;

end do;

end proc;

interval(a,b);

> integral_sost_Gaussa:=proc(a,b,c) \\подсчет интеграла

local R;

_MG(c,a,b):

_a_G(c):

W_G(x,c):

solve_w_G(x,c):

_A_G(c):

R:=_integral_G(c):

return R:

end proc;

> _integral_sost_Gaussa:=0: \\суммирование интегралов, посчитанных на разных отрезках

for i from 1 by 1 to n do

_integral_sost_Gaussa:=_integral_sost_Gaussa+integral_sost_Gaussa(a_interval[i-1],a_interval[i],m);

end do:

_integral_sost_Gaussa;

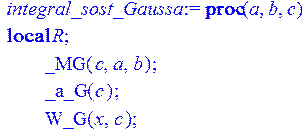
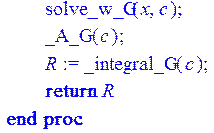
> in_3:=7.858337865;

in_6:=7.858337123;

in_12:=7.858337162;

>

H:=3;// оценка погрешности по Ричардсону

with(LinearAlgebra):

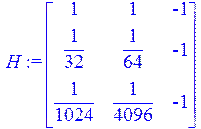
H:=Matrix([[(H/3)^5,(H/3)^6,-1],[(H/6)^5,(H/6)^6,-1],[(H/12)^5,(H/12)^6,-1]]);

Sost:=Matrix([[-in_3],[-in_6],[-in_12]]);

C_J:=Matrix(3,1):

C_J:=LinearSolve(H,Sost);

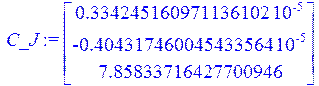
H:=3;

C1:=.334245160971136102e-5;

C2:=-.404317460045433564e-5;

> R:=C1*((H/3)^5)+C2*((H/3)^6);

R:=C1*((H/6)^5)+C2*((H/6)^6);

R:=C1*((H/12)^5)+C2*((H/12)^6);

значение, полученное через встроенные функции:

значение по ф-ле (3) -1000 значений.

по методу Гасса:

погрешность по ф-ле(27)

значения, полученные с помощью составной ф-лы Гаусса:

деление отрезка на 3 части:

деление отрезка на 6 частей:

деление отрезка на 12 частей:

погрешность по Ричардсону на основании приведенных выше разбиений:

Код программы на Си++:

Вариант Ньютона-Котеса:

#include <iostream>

#include <cmath>

#include <iomanip>

#define n 3

using namespace std;

const double a = 1.7;

const double b = 3.2;

const double alpha = 0;

const double beta = 1/4;

const double eps = 0.000001;

double node_x[n];

double mu[n];

double A_koefs[n];

double arr_x[n][n];

void gauss();

double f(double arg);

double p(double arg);

double find_mu(int deg, double a, double b);

void init_param(double a, double b);

double simple_nk(double a, double b);

double dif_nk(unsigned int k);

double find_optim();

int main()

{

int l;

cout<<setprecision(15);

simple_nk(a,b);

cout<<"Input number of nodes for composite method"<<endl;

cin>>l;

dif_nk(l);

system("pause");

return 0;

}

double f(double arg)

{