Построение полиномов Лагранжа по равностоящим и Чебышевским узлам

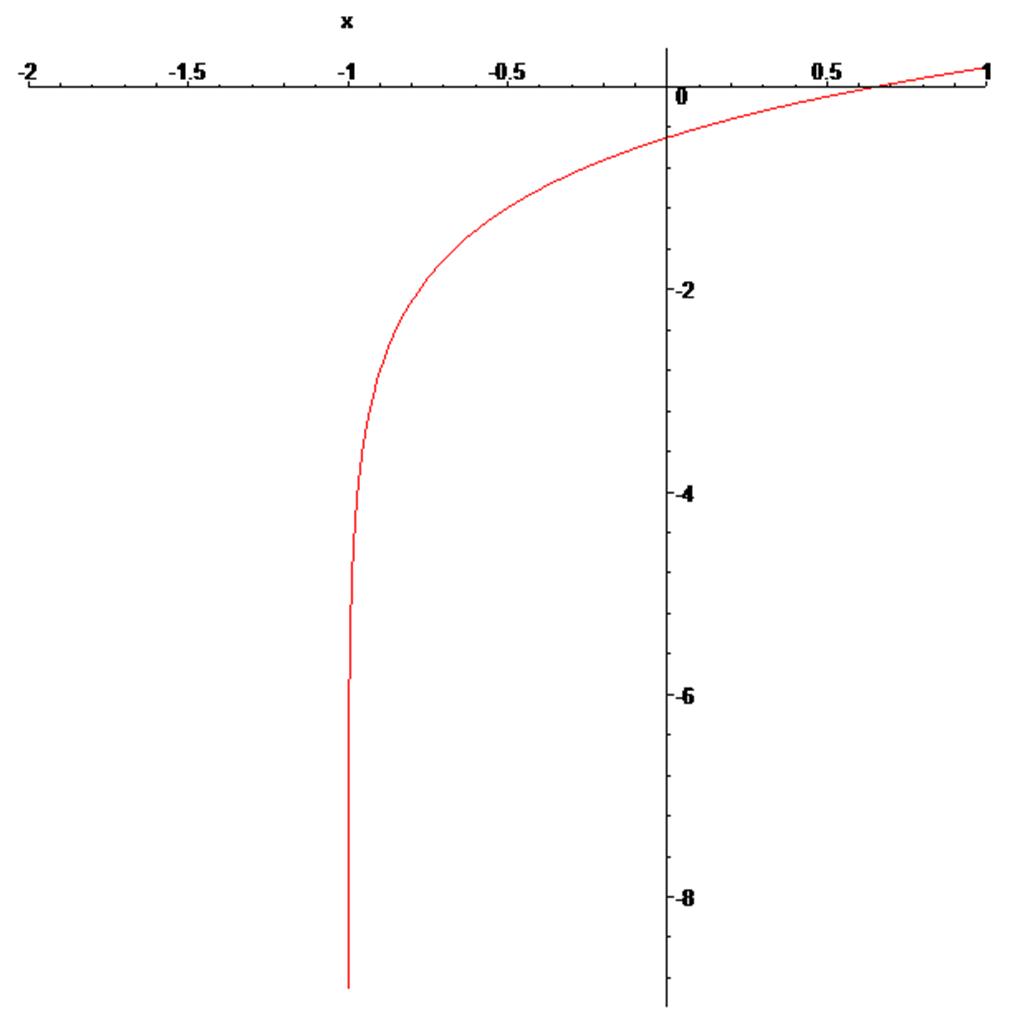
> f:=x->ln(x+1)-0.5; на основании графика выбираем интервал непрерывности [-0.9,0.9].

b:=ln(x+1)-0.5;

> plot(f(x), x=-2..1);

> рассматриваем 7 узлов-здесь считаем по Чебышеву

n:=6;

f:=x->ln(x+1)-0.5;

j:=6;for i from 0 to j do x[i]:=(1/2)*(1.8*cos(((2*i+1)/(2*n+2))*Pi)); v[i]:=evalf(x[i]); end do;

w:=product(x-v[l],l=0..n); //узловой полином

w1:=diff(w,x);// производная узлового полинома

c:=x->(x-.7036483342)*(x-.3904953655)*x*(x+.3904953655)*(x+.7036483342)*(x+.8774351210)+(x-.8774351210)*(x-.3904953655)*x*(x+.3904953655)*(x+.7036483342)*(x+.8774351210)+(x-.8774351210)*(x-.7036483342)*x*(x+.3904953655)*(x+.7036483342)*(x+.8774351210)+(x-.8774351210)*(x-.7036483342)*(x-.3904953655)*(x+.3904953655)*(x+.7036483342)*(x+.8774351210)+(x-.8774351210)*(x-.7036483342)*(x-.3904953655)*x*(x+.7036483342)*(x+.8774351210)+(x-.8774351210)*(x-.7036483342)*(x-.3904953655)*x*(x+.3904953655)*(x+.8774351210)+(x-.8774351210)*(x-.7036483342)*(x-.3904953655)*x*(x+.3904953655)*(x+.7036483342);

for k from 0 to n do L[k+1]:=w*f(v[k]) /((x-v[k])*c(v[k])); end do;считаеммножителиЛагранжа L[i], i=0..7

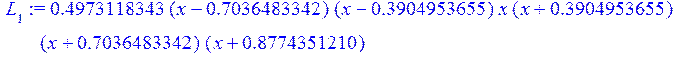
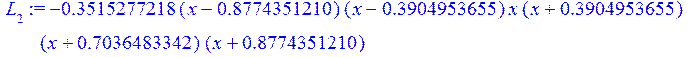
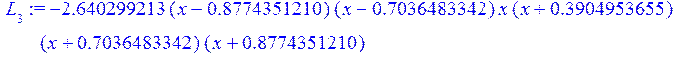
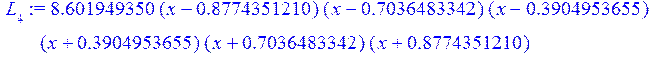
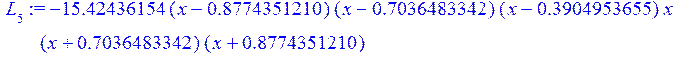
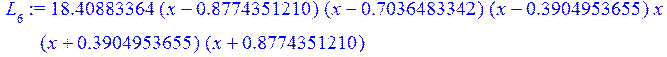
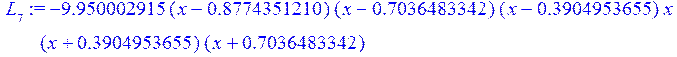
> a[1]:=collect(L[1],x);

a[2]:=collect(L[2],x);

a[3]:=collect(L[3],x);

a[4]:=collect(L[4],x);

a[5]:=collect(L[5],x);

a[6]:=collect(L[5],x);

a[7]:=collect(L[5],x);

>

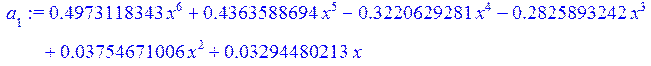
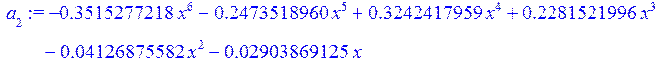
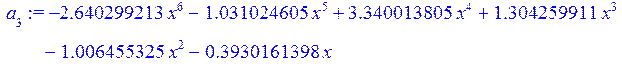
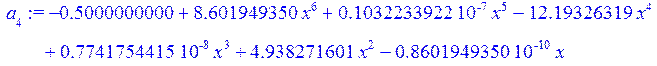
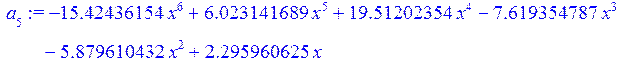
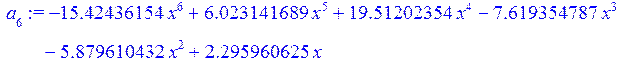
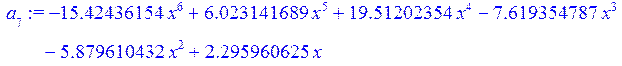
> p:=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7];

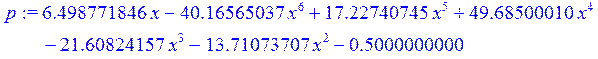
> with(plots);

> plot([b,p],x=-0.9..0.9,y=-10..10,color=[green, red]); график функции-зеленый, график приближения-красный, в узлах графики пересекаются.

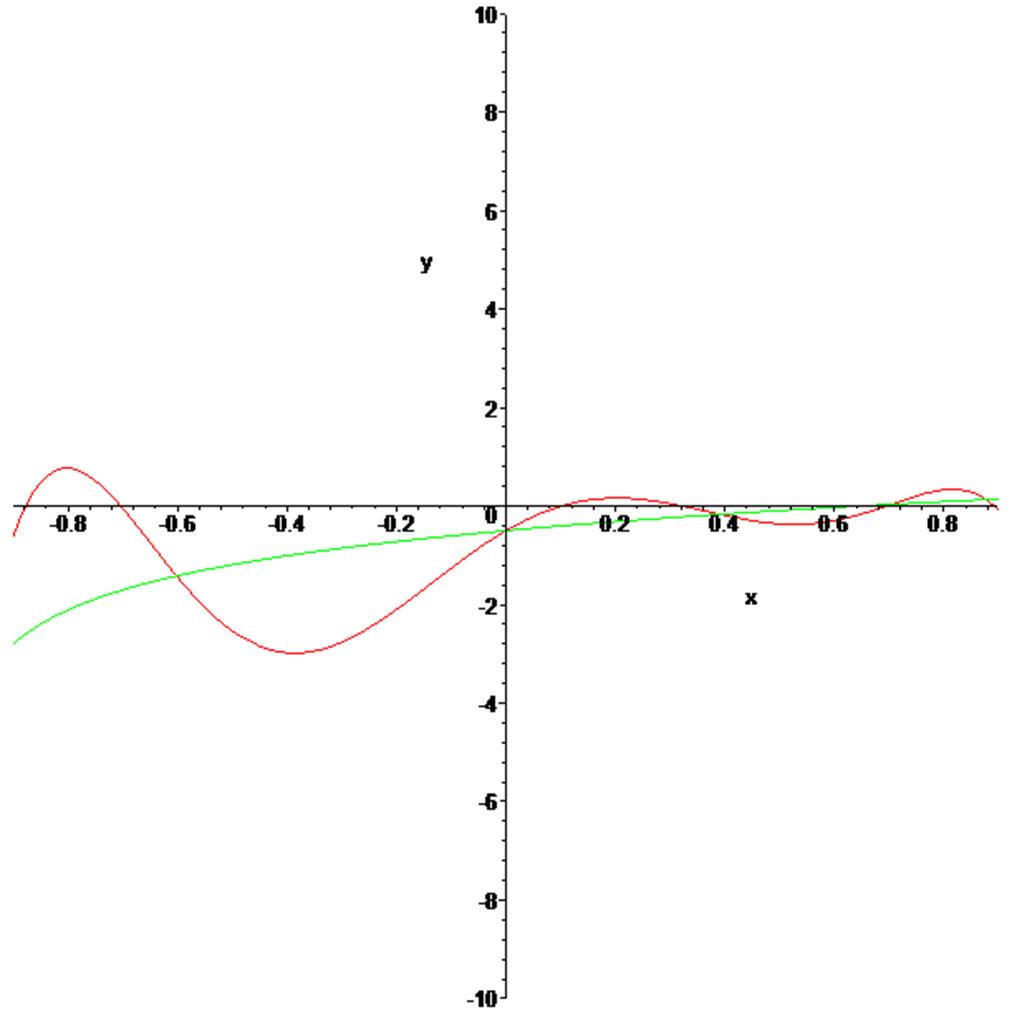
> f:=x->ln(x+1)-0.5;

b:=ln(x+1)-0.5;

> plot(f(x), x=-2..1);

>

n:=6; теперь считаем полином Лагранжа для равностоящих узлов.

f:=x->ln(x+1)-0.5;

x[0]:=-0.9; x[1]:=-0.6; x[2]:=-0.3; x[3]:=-0;x[4]:=0.3; x[5]:=0.6; x[6]:=0.9;

j:=6;for i from 0 to j do  v[i]:=evalf(x[i]); end do;

w:=product(x-v[l],l=0..n);

w1:=diff(w,x);

c:=x->(x+.6)*(x+.3)*x*(x-.3)*(x-.6)*(x-.9)+(x+.9)*(x+.3)*x*(x-.3)*(x-.6)*(x-.9)+(x+.9)*(x+.6)*x*(x-.3)*(x-.6)*(x-.9)+(x+.9)*(x+.6)*(x+.3)*(x-.3)*(x-.6)*(x-.9)+(x+.9)*(x+.6)*(x+.3)*x*(x-.6)*(x-.9)+(x+.9)*(x+.6)*(x+.3)*x*(x-.3)*(x-.9)+(x+.9)*(x+.6)*(x+.3)*x*(x-.3)*(x-.6);for k from 0 to n do L[k+1]:=w*f(v[k])

/((x-v[k])*c(v[k])); end do;

> a[1]:=collect(L[1],x);

a[2]:=collect(L[2],x);

a[3]:=collect(L[3],x);

a[4]:=collect(L[4],x);

a[5]:=collect(L[5],x);

a[6]:=collect(L[5],x);

a[7]:=collect(L[5],x);

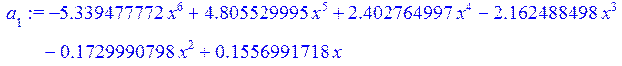
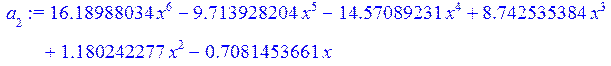
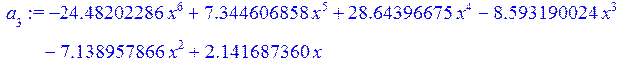
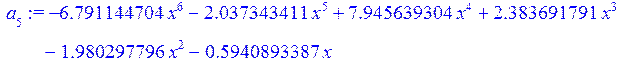
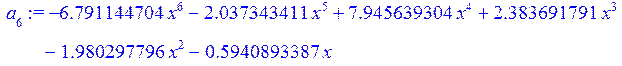
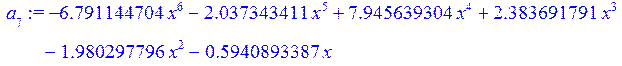
> g:=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7];

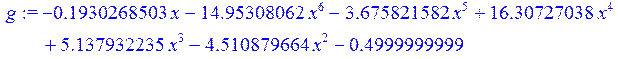
Ø  plot([b,g],x=-0.9..0.9,y=-10..10,color=[green, red]); график функции обозначен зеленым, а график приближения-красным. Получили достаточно хорошее приближение к функции.

Ø  Далее строим приближение через узлы по Чебышеву, приближение по равностоящим узлам и функцию. Видим что полином построенный по равностоящим узлам дает лучшее приближение.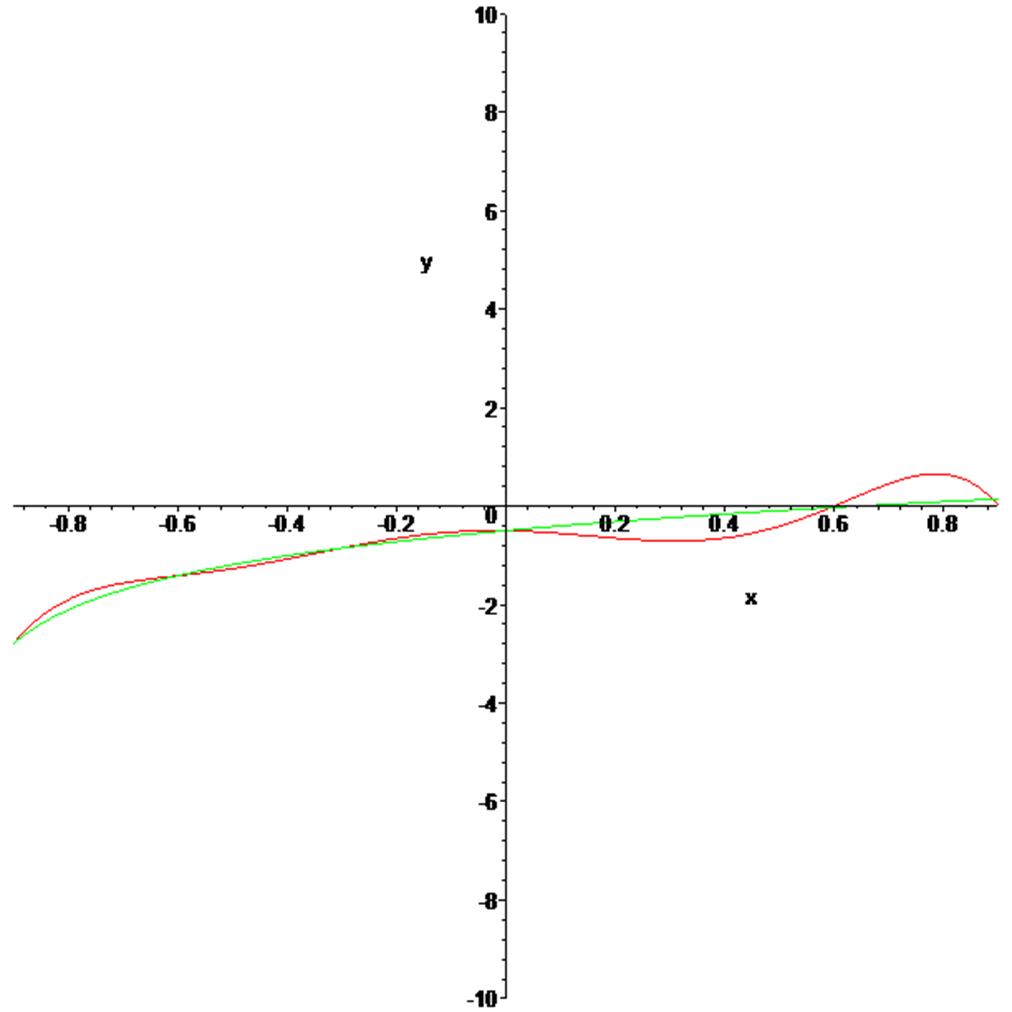

> plot([b,g,p],x=-0.9..0.9,y=-10..10,color=[green, red,yellow]);

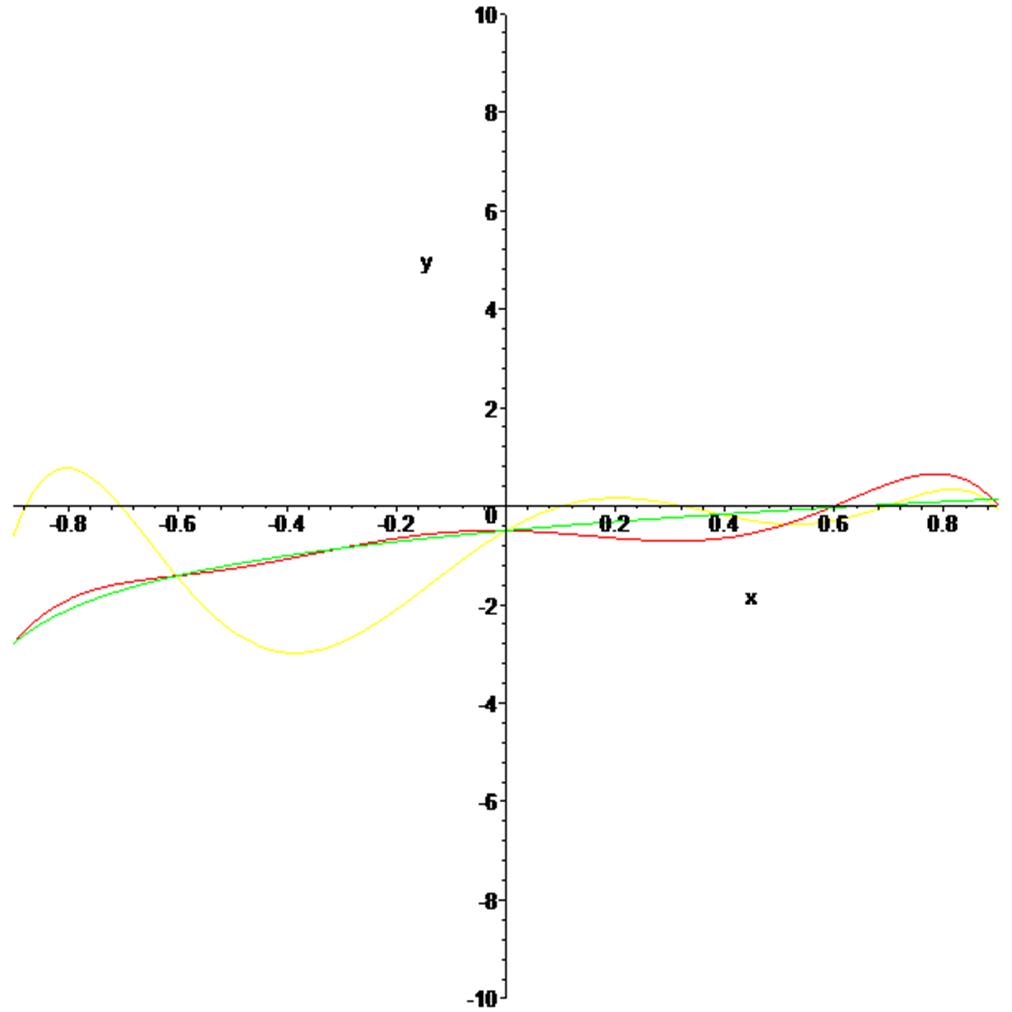
Графики для полиномов построенных по трем узлам

Значения узлов по Чебышеву:

 

Полученный полином Лагранжа:

 

Значения равностоящих узлов:

Полученный полином Лагранжа:

Ø  plot([b,g],x=-0.9..0.9,y=-10..10,color=[green, red]);

Ø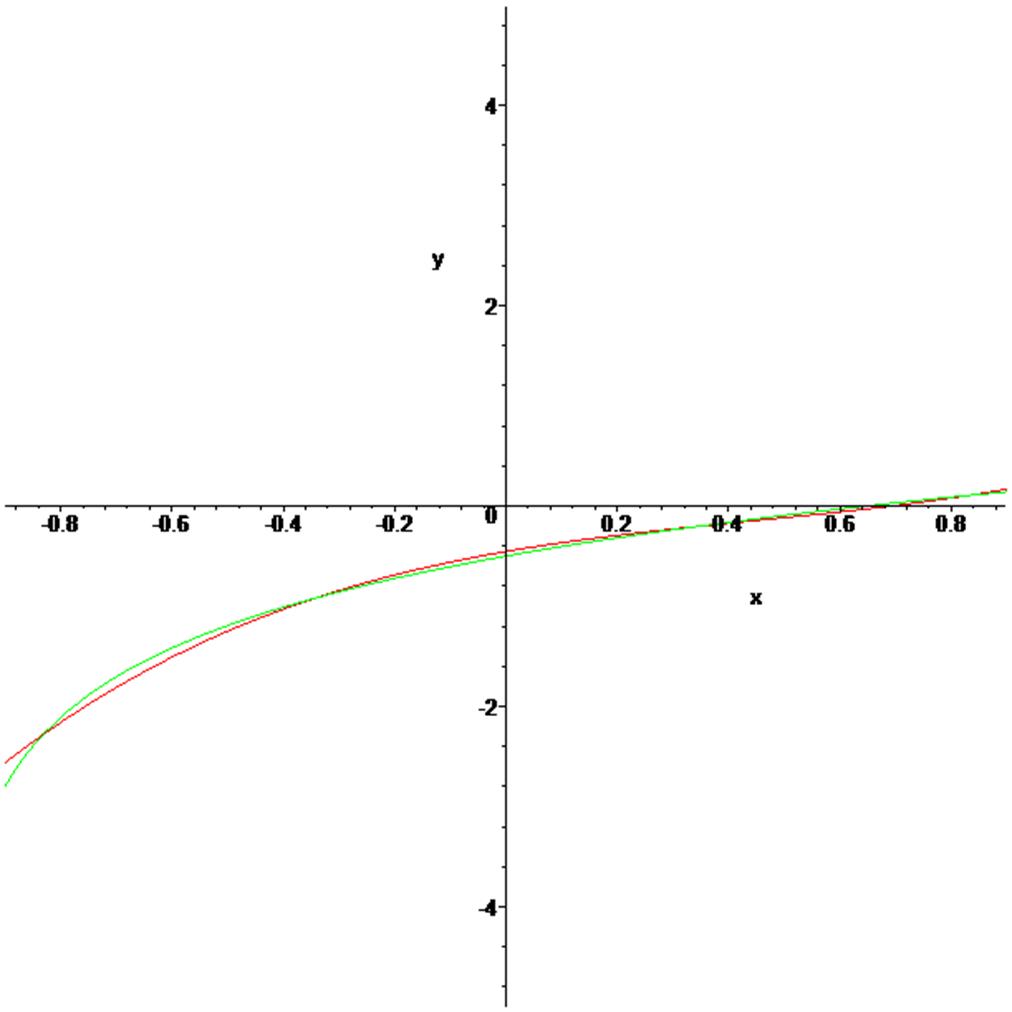 

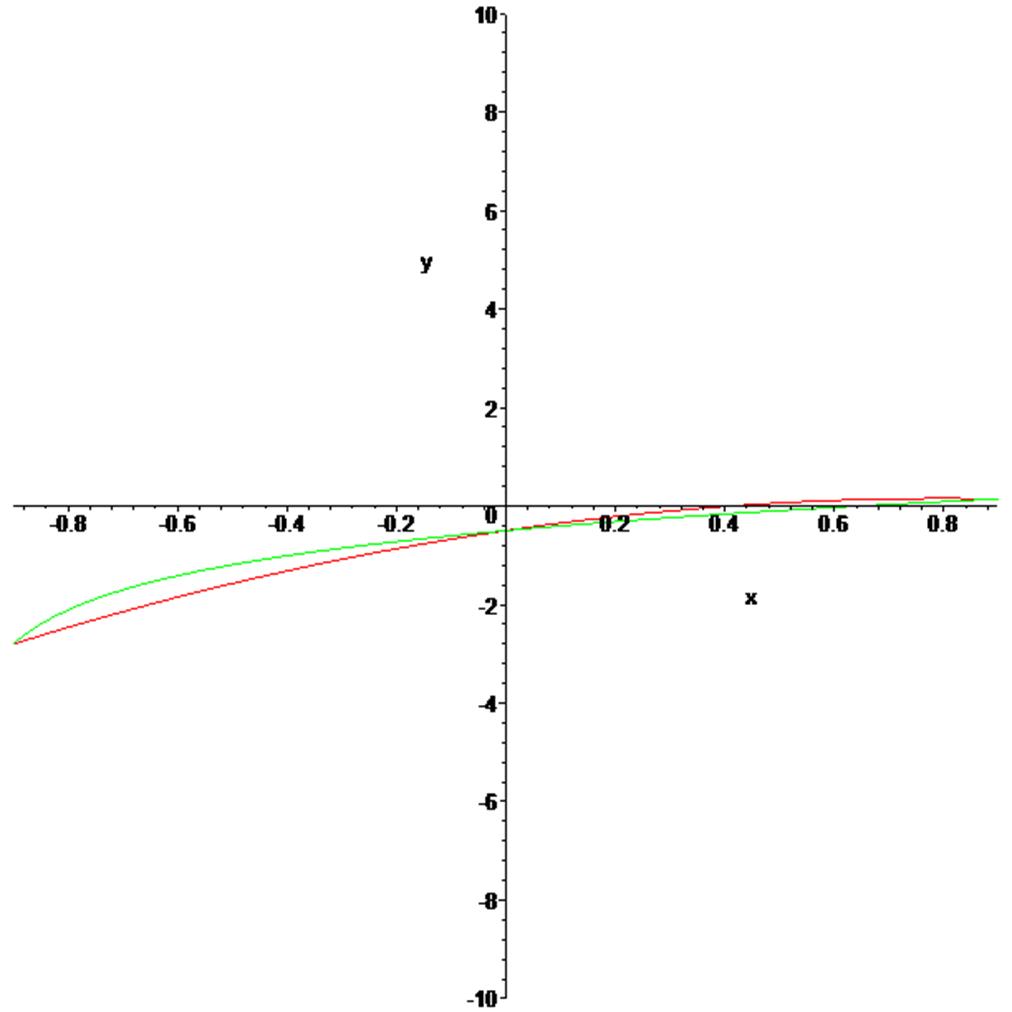
По графикам видим, что в случае трех узлов лучшее приближение дает полином, построенный по узлам Чебышева.

 Видно также, что при выборе большего числа узлов полином Лагранжа в случае равностоящих коэффициентов дает лучшее приближение. В случае же полинома Лагранжа с коэффициентами по Чебышеву такого сказать уже нельзя.

Код программы на Си++.

#include "stdafx.h"

#include <iostream>

#include <math.h>

using namespace std;

const int N=150;

int w;

const double pi=3.1415926535897932385;

#include "file.h"

void alternative()

{

cout<<"Input number 0(f(x)) or number 1(|x|*f(x))"<<'\n';

cin>>w;

}

double f(double x)//выбираем функцию

{

if (!w)

return (x*x*x-exp(x)+1);

else

return fabs(x)*(x*x*x-exp(x)+1);

}

double* uzly_ravnomerno(int s,double a,double b)//считаем узлы равностоящие друг от друга

{

double h=0,uzly[N];

h=fabs(b-a)/(s-1);

uzly[0]=a;

for(int i=1;i<s;i++)

{

uzly[i]=uzly[i-1]+h;

}

return uzly;

}

double coef_lagr_ravnomerno(double x,int s,double a,double b)//функции Лагранжа

{

double l[N],l_chisl,l_znam,lagr=0;

for (int k=0;k<s;k++)

{  

l_chisl=1;

for (int i=0;i<s;i++)

{

if (i!=k)

{

l_chisl=l_chisl*((x-uzly_ravnomerno(s,a,b)[i]));

}

}

l_znam=1;

for (int i=0;i<s;i++)

{

if (i!=k)

{

l_znam=l_znam*((uzly_ravnomerno(s,a,b)[k]-uzly_ravnomerno(s,a,b)[i]));

}

}

l[k]=l_chisl/l_znam;

}

for(int k=0;k<s;k++)

{

lagr=l[k]*f(uzly_ravnomerno(s,a,b)[k])+lagr;

}

return lagr;

}

double* uzly_po_Chebushevu(int s,double a,double b)// считаем узлы по Чебышеву

{

double uzly[N];

for (int i=1;i<=s;i++)

{

uzly[i]=(((b-a)*cos((((2*i)-1)*pi)/(2*(s)))+(b+a)))/2;

}

return uzly;

}

double coef_lagr_Chebushev(double x,int s,double a,double b) // функции Лаганжа

{

double l[N],l_chisl,l_znam,lagr=0;

for (int k=1;k<=s;k++)

{  

l_chisl=1;

for (int i=1;i<=s;i++)

{

if (i!=k)

{

l_chisl=l_chisl*((x-uzly_po_Chebushevu(s,a,b)[i]));

}

}

l_znam=1;

for (int i=1;i<=s;i++)

{

if (i!=k)

{

l_znam=l_znam*((uzly_po_Chebushevu(s,a,b)[k]-uzly_po_Chebushevu(s,a,b)[i]));

}

}

l[k]=l_chisl/l_znam;

}

for(int k=1;k<=s;k++)

{

lagr=l[k]*f(uzly_po_Chebushevu(s,a,b)[k])+lagr;

}

return lagr;

}

double* pogreshost(int q,double a,double b,int s)// погрешность для полиномов Лагранжа, построенным по равностоящим и Чебышевским узлам.(в данном случае взяли 100 точек)

{

double x[N],r_rav[N],r_cheb[N],R_rav=0,R_cheb=0,h,R[2];

h=fabs(b-a)/(q-1);

x[0]=a;

for(int i=1;i<q;i++)

{

x[i]=x[i-1]+h;

}

for (int i=0;i<q;i++)

{

r_rav[i]=fabs(f(x[i])-coef_lagr_ravnomerno(x[i],s,a,b));

r_cheb[i]=fabs(f(x[i])- coef_lagr_Chebushev(x[i],s,a,b));

if(r_rav[i]>R_rav)

R_rav=r_rav[i];

if(r_cheb[i]>R_cheb)

R_cheb=r_cheb[i];

R[0]=R_rav;

R[1]=R_cheb;

}

return R;

}

int main()

{

cout.precision(10);