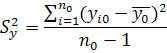
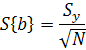
|
ŷ1 |
86,02 |
|
ŷ2 |
87,02 |
|
ŷ3 |
88,02 |
|
ŷ4 |
64,00 |
|
ŷ5 |
73,00 |
|
ŷ6 |
75,00 |
|
ŷ7 |
64,98 |
|
ŷ8 |
77,00 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.