Исследование числовых матриц на линейную независимость строк. Элементарные операции. Гауссово исключение. Преобразование Хаусхольдера. Строчно поисковый алгоритм. Форма Гейзенберга

ОСНОВНЫЕ  ОБОЗНАЧЕНИЯ

А, А(S)- матрицы числовая и ,с элементами от s

- обратная матрица

- транспонированная матрица

- определитель матрицы

-оператор дифференцирования                

-произведение матриц

-диагональная матрица

- столбцово степенная коэффициентная матрица

-единичная матрица (размером n*n)

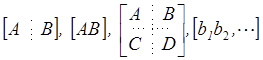-блочные матрица

≜ - знак определения

-степени полинома, строки, столбца

- ранг матрицы

-норма матрицы, вектора

s – комплексная переменная

ℂ -множество комплексных чисел

ℝ -множество вещественных чисел

ℝⁿ – множество числовых векторов размерности n

ℝ^n*m –множество вещественных матриц размерности n*m

ℝ(s) – множество передаточных функций

ℝ[s] - множество полиномов

ℝ_p(s) - множество правильных передаточных функций

ℝ^n*m[s] – множество полиномиальных матриц

ℝ^n*m(s) – множество матричных передаточных функций

min (a, b) – наименьшее из а, b

max (a, b) – наибольшее из а, b

- квантор всеобщности

- квантор существования

 - степень характеристического полинома матричной передаточной функции

1. ИССЛЕДОВАНИЕ ЧИСЛОВЫХ МАТРИЦ НА ЛИНЕЙНУЮ НЕЗАВИСИМОСТЬ СТРОК

Поиск линейно зависимых строк матрицы может быть осуществлен методом гауссова исключения, с использованием хаусхольдерова исключения и при помощи строчно поискового алгоритма. Во всех этих преобразованиях активно используется элементарные матрицы.

1.1.  Элементарные операции

Рассмотрим матрицу А с элементами в ℂ или ℝ. Следующие операции называют элементарными операциями или преобразованиями (elementary operation или transformations):

1. Умножение строки или столбца на ненулевое вещественное или комплексное число.

2. Перестановка двух строк или столбцов.

3. Сложение произведения строки или столбца на число с другой строкой или столбцом.

Эти преобразования можно выполнить, используя элементарные матрицы (elementary matrices). Пример таких матриц:

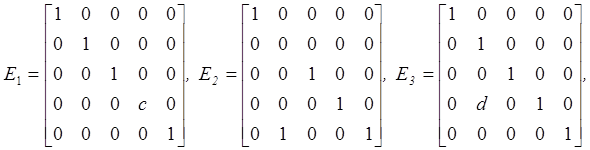
где c и d вещественные или комплексные числа и . Элементарные матрицы квадратные и несингулярные. Обратные им матрицы

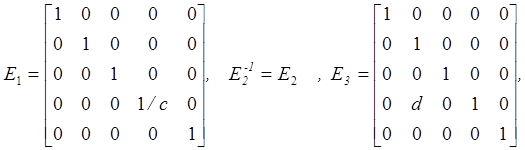
Они снова оказываются элементарными матрицами. Умножение A слева на E₁ преобразует  строки матрицы А, в то время как умножение справа матрицы А на E₁ преобразует столбцы A. Например, Е₂А переставляет вторую и пятую строки матрицы А, в то время как Е₃А добавляет произведение второй строки на dк четвертой строке А. В свою очередь АЕ₃ добавляет произведение четвертого столбца на dк второму столбцу матрицы А.

1.2.Гауссово исключение

Рассмотрим n*m матрицу

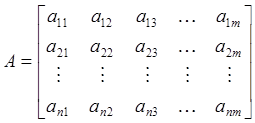.                                    (1.1)

Прежде всего, полагаем . Мы прибавим произведение первой строки на  к , тогда получим

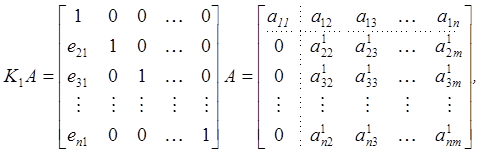                                                                  (1.2)

где e_i1=-a_i1/a₁₁ ;   и  . Отметим, что n*nматрица К₁  является произведением n-1 число элементарных матриц в форме Е₃ . Если  отлично 

от нуля, тогда добавление произведения второй строки К₁А на   к i-

строке, , приводит к

               ,                        (1.3)

где   и  . Положим в этой же манере  матрицу А, можно преобразовать  в матрицу с элементами нулевыми ниже диагонали, в то время как x обозначает, возможно

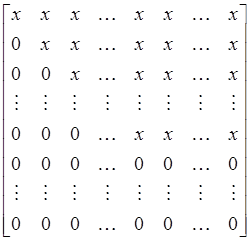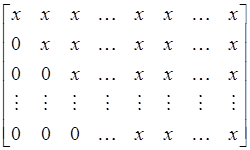          или                           (1.4)

нулевые элементы. Этот процесс преобразований называют гауссовым исключением ( gaussian elimination ). Матрицы в (1.4) верхнетреугольные.

Эта процедура нарушится, если какой-либо из элементов   станет равным нулю. Даже если все эти элементы будут ненулевые, могут  возникнуть вычислительные трудности. Вычислительные ошибки будут расти, если диагональные элементы малы. Ввиду этого явления процедура гауссова исключения может быть численно неустойчива.

Для того чтобы обойти эту трудность, перед проведением процедуры вычислений мы должны найти элемент с наибольшей по модулю величиной в первом столбце А и затем переставить строку матрицы с этим элементом на место первой, используя  матрицу вида Е₂ . Затем проводим процедуру  исключения для первого столбца. Перед выполнением исключения во втором столбце  найдем наибольший по модулю элемент во втором столбце К₁А, за исключением первого элемента, и переведем его на место . Эту процедуру исключения называют гауссовым  исключением с частичным упорядочением (gaussian elimination with partial pivoting). В данной процедуре имеем  , и  ошибки не возрастают. Следовательно, эта процедура более устойчива по сравнению гауссовым исключением.

Устойчивость гауссова исключения может быть еще улучшена посредством полного упорядочения (complete pivoting). В этом случае мы должны применять элементарные строчные операции, так же как перед этим использовали элементарные столбцовые  операции. Прежде всего находим наибольший по модулю элемент среди всех элементов матрицы  А. Затем перемещаем этот элемент в первый  столбец  при помощи элементарных столбцовых операций и далее в первую строку посредством  элементарных строчных операций. Далее выполняем, процедуру исключения в первом столбце, преобразуя А. После этого исключения повторяем процедуру над оставшейся матрицей. Эта процедура обладает наибольшей численной устойчивостью по сравнению с частичным упорядочением, но она более трудоемкая , так как требует поиска наибольшего по модулю элемента.

1.3. Преобразование Хаусхольдера