Соединение “звеньев” и свойства. Взаимно связанные системы, замкнутость, разомкнутость, хорошая устроенность полиномиального матричного описания

5.  СОЕДИНЕНИЕ “ЗВЕНЬЕВ” И СВОЙСТВА

Взаимно связанные системы, замкнутость, разомкнутость, хорошая устроенность полиномиального матричного описания.

Систему с многими входами и выходами с довольно сложной структурой, например как в $26, можно представить в стандартном виде (рисунок из S112). Для последней рассматривается ряд различных предположений: ВС - взаимосвязанности S112; ХУ - хорошей устроенности S114; ХУМПО - хорошей устроенности полиномиального матричного описания S15. При различных комбинациях этих предположений изучаются свойства систем.

S112.  Предположение ВС: рассматриваем взаимосвязанную систему (interconnected system). Предполагаем ее состоящей из пропорциональных “звеньев” , динамических “звеньев”, описываемых передаточными функциями , и суммирующих узлов 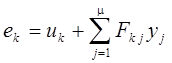. Считаем, что суммирующий узел стоит на входе динамического звена .

Введем обозначение:

,

.

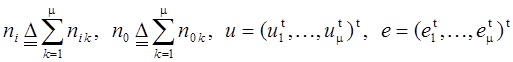С учетом введенных обозначений взаимосвязанная система будет описываться следующими уравнениями:

                                                         ,                                                     (а)

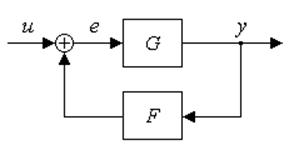что соответствует структурной схеме

$26. 

Систему где  - векторы размерности , а  - векторы размерности , описать уравнениями (а) из S112. В данном случае

,

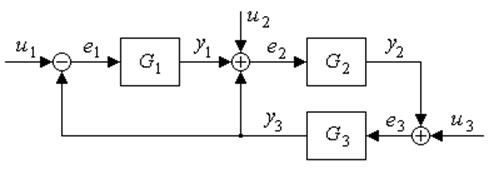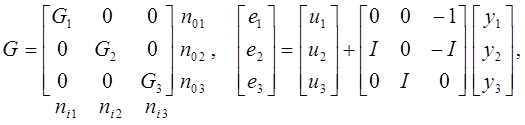
так как , , .

S113.  Рассмотрим две передаточные функции оп структуре рисунка S112.

Передаточную функцию “вход u” / “выход е” -  называют функцией вход-ошибка (input-error function); очевидно, что

                                                  .                                            (а)

Передаточную функцию “вход u” / “выход y” -  называют функцией вход-выход (input-output function); найдем ее:

, откуда  или ; окончательно

                                                         .                                                    (б)

$27.  Показать, что

.

Подсказка. Выражение  умножить справа на .

S114.  Предположение ХУ (well posedness): предполагаем, что система, изображенная на рисунке S112, удовлетворяет ВС и еще условию

.

(Смысл этого предположения в том, что передаточные функции между любыми двумя точками этой системы - правильные).

S115.  ПредположениеХУМПО (well posedness of polynomial matrix description): рассматриваем систему S112. Для всех передаточных функций  дано полиномиальное матричное разложение . Более подробно: дано

.

Предполагается, что  хорошо сформирована, нет скрытых неустойчивых мод. Кроме того, .

S116.  Предположение ХУМПО равносильно тому, что для всякого  имеется приведенное левое разложение  такое, что:

1)   внутренне правильное левое разложение ;

2)  ;

3)  .

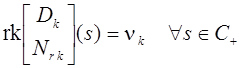S117.  Можно перейти к полиномиальному матричному описанию в системе, приведенной в S112. Введем обозначения:

,

,

,

.

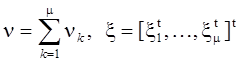С учетом этих обозначений получаем полиномиальное матричное описание для системы, изображенной на рисунке S112, а именно . Передаточную функцию G можем вычислить, как , а полиномиальное описание записывается стандартным образом:

                                   .                              (а)

Это описание называют полиномиальным матичным описанием разомкнутой системы (open-loop PMD) и обозначают . Разомкнута обратная связь F (на рисунке S112).

S118.  Пусть система (а) S117, соответствующая S112, удовлетворяет предположениям ВС, ХУ, ХУМПО. Тогда эта система хорошо устроена и у нее нет скрытых неустойчивых мод.

S119.  Пусть выполняются предположения ВС, ХУ и ХУМПО. Рассмотрим замкнутую систему S112 (замкнуто F). Полиномиальному матричному описанию замкнутой системы “вход-выход” (closed-loop input-output PMD) соответствуют уравнения

, где

                                                    .                                              (а)

Говорят, что задана замкнутая система . Следовательно, передаточная функция  равна.

                                                            .                                                       (б)

$28.  Показать, что формула (а) из S119 справедлива. Покажем возможное решение. Из рисунка S112:

                                                                 ,                                                            (б)