![]() , (в)
, (в)
![]() .
(г)
.
(г)
S120.
Рассмотрим две передаточные функции
замкнутой системы ![]()
![]()
и ![]()
![]() , т.
е. мы рассматриваем систему, изображенную на рисунке, приведенном в S112. Пусть эта система удовлетворяет предположениям ВС,
ХУ и ХУМПО. Тогда
, т.
е. мы рассматриваем систему, изображенную на рисунке, приведенном в S112. Пусть эта система удовлетворяет предположениям ВС,
ХУ и ХУМПО. Тогда ![]() хорошо устроены.
хорошо устроены.
Доказательство. Покажем, что ![]() - правильная. Из S118 следует,
что
- правильная. Из S118 следует,
что ![]() хорошо
устроена, т. е. левое-правое разложение
хорошо
устроена, т. е. левое-правое разложение ![]() внутренне правильное. Из S111 можем утверждать, что D
раскладывается в произведение
внутренне правильное. Из S111 можем утверждать, что D
раскладывается в произведение ![]() , где
, где ![]() - полиномиальная столбцово приведенная матрица,
- полиномиальная столбцово приведенная матрица, ![]() - биправильная матричная передаточная функция,
- биправильная матричная передаточная функция, ![]() - полиномиальная строчно приведенная матрица. Матрицу G
можем преобразовать так:
- полиномиальная строчно приведенная матрица. Матрицу G
можем преобразовать так:
![]() .
.
В S111 утверждается, что
![]() ,
, ![]() - (а)
- (а)
правильные
передаточные функции, а так как ![]() биправильная, то G
правильная. Но
биправильная, то G
правильная. Но ![]() , что следует из (а) S119. Тогда
, что следует из (а) S119. Тогда
![]() . (б)
. (б)
![]() .
(в)
.
(в)
S121.
Пусть полиномиальное матричное
описание системы S112
“вход-выход” удовлетворяет всем предположениям: ВС, ХУ, ХУМПО. Тогда ![]() хорошо устроено, а Dyu не имеет
неустойчивых скрытых мод.
хорошо устроено, а Dyu не имеет
неустойчивых скрытых мод.
При данных условиях S118 Dyе не
имеет скрытых мод в ![]() , что
равносильно условиям S116, S117:
, что
равносильно условиям S116, S117:
![]() ,
(а)
,
(а)
![]() .
(б)
.
(б)
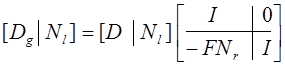 .
(в)
.
(в)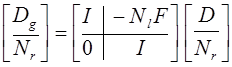 ,
,Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.