Численная устойчивость исключения может быть улучшена благодаря использованию преобразованияХаусхольдера (Householder transformation). Пусть I будет устойчивой матрицей. Преобразованием Хаусхольдера называется квадратная матрица вида
![]()
с ххt=1, где х- столбцовый вектор и хtего транспонирование. Очевидно, что
![]() ,следовательно,
Hсимметричная
матрица. Ввиду этого , а также используя ххt=1, получим
,следовательно,
Hсимметричная
матрица. Ввиду этого , а также используя ххt=1, получим
![]() , т.е. H-1=Ht, следовательно, H –
ортогональная матрица. Поэтому все сингулярные значения Hравны 1 и
ее число обусловленности (condition number), определенное как
отношение наибольшего и наименьшего сингулярных значений , равно 1. Таким образом,
использование преобразования Хаусхольдера не ухудшает численные свойства
задачи.
, т.е. H-1=Ht, следовательно, H –
ортогональная матрица. Поэтому все сингулярные значения Hравны 1 и
ее число обусловленности (condition number), определенное как
отношение наибольшего и наименьшего сингулярных значений , равно 1. Таким образом,
использование преобразования Хаусхольдера не ухудшает численные свойства
задачи.
Важное свойство
преобразования Хаусхольдера состоит в том, что для заданных двух векторов a
и b с равными нормами Эвклида ![]() существует
преобразование Хаусхольдера Н такое , что На=b.
Действительно, если выберем
существует
преобразование Хаусхольдера Н такое , что На=b.
Действительно, если выберем ![]() , то
, то
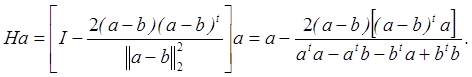
Так как ![]() по предположению и
по предположению и ![]() ввиду независимости скалярного
произведения от транспонирования, имеем
ввиду независимости скалярного
произведения от транспонирования, имеем
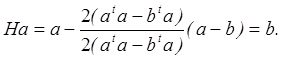
Это доказывает утверждение. Сейчас, используя данное свойство, покажем, что К1 и К2 в (1.2) и (1.3) могут быть выбраны как преобразования Хаусхольдера.
Рассмотрим n*m матрицу А заданную в(1.1). Прежде всего вычислим норму σ первого столбца а1 матрицы А. Выберем b1 равным
![]()
Тогда существует преобразование Хаусхольдера Н1 такое, что Н1А будет иметь форму, показанную в первой части (1.2). Далее мы исключаем первый столбец и первую строку Н1А и повторим процедуру для первого столбца оставшейся подматрицы . Поступая подобным образом , матрица А может быть преобразована последовательностью хаусхольдеровых преобразований к форме (1.4).
Численная устойчивость этого процесса может быть далее улучшена перестановкой столбцов. Вначале мы вычисляем норму всех столбцов А. Далее переставляем столбец с наибольшей нормой с первым столбцом. Далее применяем хаусхольдерово преобразование, что соответствует исключению. Подобным образом диагональные элементы результирующей матрицы будут располагаться в порядке убывания по амплитуде. Назовем этот процесс преобразованием Хаусхольдера с упорядочением (Householder transformation with pivoting).
Отметим, что хаусхольдерово преобразование не приводит матрицу к треугольному виду. Следовательно, строки матрицы А полностью перемещаются.
1.4. Строчно поисковый алгоритм
В приложениях очень часто требуется провести исследование строк некоторой матрицы А на линейную независимость в направлении сверху вниз. Для этого мы прежде всего проверяем будет ли первая строка ненулевой, т.е. линейно независимой от себя. Мы затем проверяем будет ли вторая строка линейно независимой от первой строки. На к-м шаге мы проверяем будет ли к- строка А линейно независимой от ее предыдущих к-1 строк, то эта строка должна быть исключена из последующего рассмотрения. Далее нам может потребоваться найти коэффициенты, обеспечивающие линейную зависимость этих строк.
Пусть (i,j)- й элемент n*m матрицы А обозначен аij . Пусть а1к будет некоторой ненулевой элемент первой строки матрицы А. Этот элемент будет называть ведущим элементом (pivot element) или просто ведущим (pivot). Введем матрицы
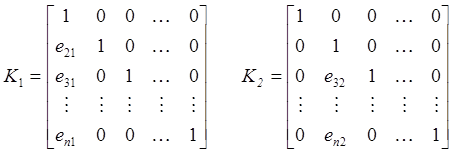
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.