Исследование числовых матриц на линейную независимость строк. Элементарные операции. Гауссово исключение. Преобразование Хаусхольдера. Строчно поисковый алгоритм. Форма Гейзенберга, страница 4

Этот алгоритм исследует линейную независимость, строк А, последовательно начиная от первой строки, второй строки и так далее, из-за чего  его и назвали строчно-поисковым алгоритмом  (row-searching algorithm). В этом алгоритме, если i-я строка линейно зависима , то i-я строка не вводится в линейную комбинацию  j-й линейно зависимой строки  при  j > i. В примере, так как а₃ линейно зависима, ее коэффициент в (1.12) равен нулю; следовательно, выражено как линейная комбинация  ее предыдущих линейно независимых строк. В общем случае, если i-я строка линейно зависима, то i-я строка  есть нулевая строка, и К_i  в  (1.10) – единичная матрица. Обратно, все элементы  ниже е_ii в i-м столбце А нули. Таким образом, е_pi=0 для  . Следовательно, из (1.9) получаем b_ji=0. Ввиду этого свойства b_jk, вычисленные по этому алгоритму, единственны. Без b_ji=0. Коэффициенты комбинаций могут быть неединственны. Например, сложив (1.11) и (1.12), получим

где не выполняются  b₅₃= 0  и  соответствует новой комбинации.

Сделаем замечание о численной устойчивости строчного поискового алгоритма. Можно выбрать ведущий элемент как самый левый ненулевой элемент строки. Но можно выбрать его как самый большой по модулю элемент строки. Но тогда он не будет самым большим элементом столбца. Следовательно, этот алгоритм может быть численно неустойчивым.

При поиске линейно зависимых строк  важно не менять порядок строк. Положение столбцов, однако, может быть произвольно изменено. Таким образом, мы можем к столбцам А применять гауссово исключение с частичной выборкой ведущих элементов или преобразование  Хаусхольдера для приведения А к нижнетреугольному виду:

≜.                                (1.13)

Здесь L_i- элементарные матрицы или хаусхольдеровы преобразования (но перестановки строк здесь недопустимы). Предлагается, что Ясно, что из (1.13) следует, что первая и пятая строка А линейно независимы от их предыдущих строк. Для того чтобы найти коэффициенты линейной комбинации для третьей строки, решим

,

что влечет

Для определения коэффициентов линейной комбинации пятой строки решим

что влечет

1.5.  Форма Гейзенберга

Любую квадратную матрицу можно преобразовать к жордановому каноническому виду. Однако это требует вычисления собственных векторов  и собственных значений, что приводит к не совсем удобным  в смысле  численной устойчивости алгоритмам. Ниже мы используем элементарные матричные преобразования  к специальному виду, называемому формой Гейзенберга (Hessenberg form). Эта форма часто используется, например, при поиске линейно независимых строк или столбцов (определение ранга матрицы наблюдаемости, управляемости и так далее).

Пусть матрица А имеет размерность n*n. Рассмотрим

  ≜

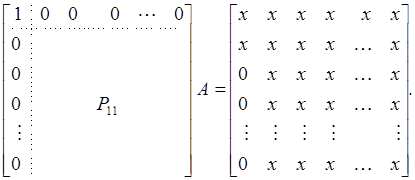
Здесь матрица P₁₁ выбрана так, что первый столбец А, за исключением двух  первых элементов, равен нулю. Это можно достичь, используя гауссово исключение с частичным упорядочением или преобразованием Хаусхольдера. Обращение А имеет такую же  форму, что и P₁. Умножение P₁Aсправа на  не изменяет первый столбец P₁A; следовательно, набор нулей в первом столбце P₁A сохраняется и в . Далее находим P₂ такую, чтобы

≜ 

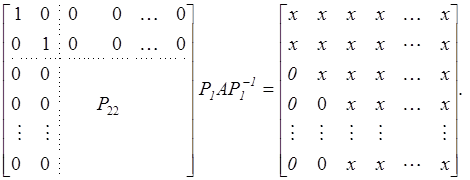
Опять же такая матрица обратная от P₂  имеет форму  аналогичную P₂ и  умножение справа  на  не влияет на первые два столбца . Следовательно, набор нулей в первых двух столбцах  будет сохранен  и в . Поступая аналогичным образом, мы можем преобразовать матрицу последовательностью аналогичных преобразований к форме

.                                     (1.14)

Она называется верхней формой Гейзенберга (upper Hessenberg form) и может быть получена устойчивыми  в вычислительном отношении методами. Эта форма очень полезна  во многих компьютерных вычислениях.