При ![]() матрицу
матрицу
![]() называют строго правильной
(strictly proper)
и обозначают
называют строго правильной
(strictly proper)
и обозначают ![]() .
.
S35. Возьмем
полиномиальный вектор ![]() размерности
n. Степенью вектора m (degree of m)
называется наивысшая степень из всех элементов вектора m
и обозначается так:
размерности
n. Степенью вектора m (degree of m)
называется наивысшая степень из всех элементов вектора m
и обозначается так: ![]() .
.
Используется понятие степени
строки (row-degree) матрицы
![]() . Степень i - й строки матрицы М обозначается:
. Степень i - й строки матрицы М обозначается: ![]() . Аналогично вводится степень столбца
(column-degree) -
. Аналогично вводится степень столбца
(column-degree) - ![]() .
.
$9. Для
нулевого вектора ![]() принято считать, что
принято считать, что ![]() . Попробуйте объяснить, почему именно так
выбрали.
. Попробуйте объяснить, почему именно так
выбрали.
S36. Для правильной
матрицы ![]() при взаимно простом
правом полиномиальном разложении
при взаимно простом
правом полиномиальном разложении ![]() имеет
место
имеет
место
![]() ,
(а)
,
(а)
а для строго правильной
![]() .
(б)
.
(б)
$10. Обратное утверждение не имеет места, т. е. из (а) пункта S36 не следует правильность матрицы. Для передаточной функции
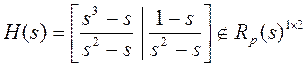
дано разложение
 .
.
Проверить (а), (б) из S36. Является ли это разложение взаимно простым?
S37. Полиномиальная
матрица ![]() называется столбцово
приведенной (column-reduced),
если
называется столбцово
приведенной (column-reduced),
если
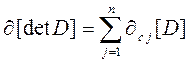 , и строчно приведенной (row-reduced), если
, и строчно приведенной (row-reduced), если
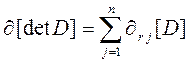 .
.
$11. Показать, что
 . (а)
. (а)
У к а з а н и е. Обозначим ![]() - это
наивысшая степень элемента j-того столбца матрицы D. Если
окажется, что хотя бы в двух столбцах матрицы D, например,
в i-м и j-м, наивысшие степени
- это
наивысшая степень элемента j-того столбца матрицы D. Если
окажется, что хотя бы в двух столбцах матрицы D, например,
в i-м и j-м, наивысшие степени ![]() и
и ![]() попадут
с одну строку, то в правой части (а) сумма будет больше порядка
детерминанта. Детерминант – это сумма произведений элементов из разных столбцов
и строк!
попадут
с одну строку, то в правой части (а) сумма будет больше порядка
детерминанта. Детерминант – это сумма произведений элементов из разных столбцов
и строк!
$12.
Подсчитать ![]() и
и  для
для
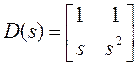 .
.
У к а з а н и е. Первый столбец умножить на sи вычесть из второго столбца. Будет ли матрица столбцово приведенной? Записать матрицу, соответствующую этой операции. (Элементарными операциями любую матрицу можно привести к приведенному виду!)
S38.
Для несингулярной матрицы ![]() обозначим
обозначим ![]() .
Пусть матрица D такая, что
.
Пусть матрица D такая, что
![]() , т.е.
элементы матрицы
, т.е.
элементы матрицы ![]() -
конечные числа. Эта матрица называется матрицей коэффициентов при высших
столбцовых степенях (highest column-degree
coefficient matrix). Это коэффициенты при
-
конечные числа. Эта матрица называется матрицей коэффициентов при высших
столбцовых степенях (highest column-degree
coefficient matrix). Это коэффициенты при ![]() элементов
элементов ![]() матрицы
D
матрицы
D ![]() .
.
S39. Для столбцово приведенной матрицы D(s) (в основном мы пишем D вместо D(s)) имеет место равенство
 .
.
S40.
Для несингулярной матрицы ![]() вычислим
вычислим ![]() и
и ![]() . Следующие утверждения эквивалентны:
. Следующие утверждения эквивалентны:
1) D – столбцово приведенная;
2)
![]() - невырожденная;
- невырожденная;
3)
предел ![]() равен невырожденной матрице
равен невырожденной матрице ![]() .
.
S41.
Дано правое разложение ![]() матрицы
матрицы ![]() , где
, где ![]() - столбцово приведенная. Тогда
- столбцово приведенная. Тогда ![]() правильная
правильная ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]() имеет место
имеет место
![]() .
.
S42.
Если столбцово приведенные
несингулярные полиномиальные матрицы ![]() эквивалентны справа,
тогда их столбцовые степени совпадают. Предполагается, что мы их упорядочили,
например, по возрастанию.
эквивалентны справа,
тогда их столбцовые степени совпадают. Предполагается, что мы их упорядочили,
например, по возрастанию.
S43.
Пусть ![]() - несингулярная. Тогда для
- несингулярная. Тогда для ![]() справедливо следующее:
справедливо следующее:
1)
$! (существуют единственные) Qr и Rr размером ![]() такие,
что
такие,
что ![]() . По существу рассматриваем
операцию ”деления”:
. По существу рассматриваем
операцию ”деления”:
![]() .
(а)
.
(а)
2)
Если ![]() -
столбцово приведенная и
-
столбцово приведенная и ![]() справедливо
справедливо
![]() , тогда
Qr и Rr – единственные.
, тогда
Qr и Rr – единственные.
$$13. Записать формулу “деления” для левого разложения, аналогичную формуле правого деления S43, а. Показать, что:
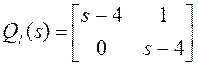 ,
,  , если
, если
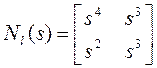 ,
,  .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.