Часто используется матрица ![]() . Она также имеет блочный вид:
. Она также имеет блочный вид:
![]()
![]()
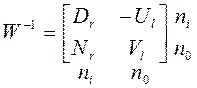
Размеры блоков указаны. Так как ![]() , имеем
, имеем
![]()
![]()
![]()
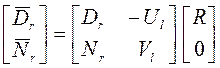 , откуда
, откуда ![]() ,
, ![]() . Процедура поиска правого взаимно простого
разложения состоит в поиске матрицы W,
соответствующей приведению матрицы М к верхнетреугольному виду, а затем
вычислению матрицы
. Процедура поиска правого взаимно простого
разложения состоит в поиске матрицы W,
соответствующей приведению матрицы М к верхнетреугольному виду, а затем
вычислению матрицы ![]() , левые
блоки которой соответствуют левому взаимно простому разложению.
, левые
блоки которой соответствуют левому взаимно простому разложению.
$4. Укажите размеры матриц, составляющих матрицу W.
$5. Покажите, что:
1) ![]() ;
;
2) наибольший общий
правый делитель пары матриц ![]() есть R.
есть R.
$6. Наити наибольший общий правый делитель матриц:
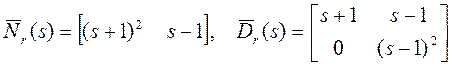 .
.
![]()
![]() Возможное
решение:
Возможное
решение:
![]()
![]()
 .
.
S22. Пусть ![]() ,
, ![]() - наибольшие общие делители матриц
- наибольшие общие делители матриц ![]() , тогда матрицы
, тогда матрицы ![]() , R2
унимодальны, что записывается так:
, R2
унимодальны, что записывается так: ![]() ~ R2.
~ R2.
S23. Тождество Безу
(Bezout identity).
Пусть ![]() и
и ![]() . Тогда
. Тогда ![]() -
взаимно простые, если и только если существуют такие унимодальные матрицы
-
взаимно простые, если и только если существуют такие унимодальные матрицы ![]() (символом “E”обозначают то, что матрицы берутся соответствующих размеров), что имеет
место равенство
(символом “E”обозначают то, что матрицы берутся соответствующих размеров), что имеет
место равенство ![]() .
.
S24. ![]() -
взаимно простые, если и только если
-
взаимно простые, если и только если
![]()
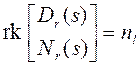 .
.
S25. Пару матриц ![]() элементарными операциями над строками, что
соответствует умножению слева на унимодальную матрицу W,
можем привести к нижнетреугольному виду
элементарными операциями над строками, что
соответствует умножению слева на унимодальную матрицу W,
можем привести к нижнетреугольному виду
![]()
![]()
 .
.
Здесь матрица W разбита на блоки (аналогично S21).
S26. Для матричной
передаточной функции (transfer function matrix)
![]() возьмем пару матриц
возьмем пару матриц
![]() (а)
(а)
такую, что матрицы ![]() - взаимно простые справа и
- взаимно простые справа и ![]() ,
, ![]() .
Запись вида (а) равносильна записи:
.
Запись вида (а) равносильна записи: ![]() ,
, ![]() .
Такая пара матриц (
.
Такая пара матриц (![]() ) называется правым взаимно простым разложением матрицы Н (right coprime fraction).
) называется правым взаимно простым разложением матрицы Н (right coprime fraction).
Аналогично введем пару матриц
![]()
такую, что матрицы ![]() - взаимно простые слева и
- взаимно простые слева и ![]() ,
, ![]() .
Такая пара матриц (
.
Такая пара матриц (![]() ) называется левым взаимно простым разложением матрицы Н (left coprime fraction).
) называется левым взаимно простым разложением матрицы Н (left coprime fraction).
S27. ![]() существует правое взаимно простое
разложение (
существует правое взаимно простое
разложение (![]() ). Запись “
). Запись “![]() ” читается так: “для любой
матричной передаточной функции”.
” читается так: “для любой
матричной передаточной функции”.
S28. (![]() ) -
правое взаимно простое разложение тогда и только тогда, когда существуют
унимодальные матрицы
) -
правое взаимно простое разложение тогда и только тогда, когда существуют
унимодальные матрицы ![]() такие,
что
такие,
что
![]() .
.
(![]() ) - левое взаимно простое разложение тогда и
только тогда, когда существуют унимодальные матрицы
) - левое взаимно простое разложение тогда и
только тогда, когда существуют унимодальные матрицы ![]() такие, что
такие, что
![]() .
.
$7. Показать,
что ![]() -
это правое взаимно простое разложение некоторой матричной передаточной функции.
-
это правое взаимно простое разложение некоторой матричной передаточной функции.
S29. Пусть для ![]() даны два взаимно простых правых разложения
(
даны два взаимно простых правых разложения
(![]() ), (
), (![]() ). Тогда существует унимодальная матрица R такая, что
). Тогда существует унимодальная матрица R такая, что ![]() ,
, ![]() .
.
Доказательство.
Воспользуемся (S28): существуют такие
матрицы ![]() ,
, ![]() ,
, ![]() ,
,
![]() , что
, что
![]() ,
(а)
,
(а)
![]() .
(б)
.
(б)
Но ![]() ,
откуда
,
откуда ![]() , где
, где ![]() . Точно так же можно показать, что
. Точно так же можно показать, что ![]() . Осталось показать, что R унимодальная матрица. Умножим (а) справа на
. Осталось показать, что R унимодальная матрица. Умножим (а) справа на ![]() :
:
![]() .
.
Но ![]() ,
, ![]() , поэтому предыдущее уравнение эквивалентно
, поэтому предыдущее уравнение эквивалентно
![]() . Следовательно, матрица R полиномиальная. Ранее было показано, что
. Следовательно, матрица R полиномиальная. Ранее было показано, что ![]() ,
, ![]() ,
откуда
,
откуда ![]() ,
, ![]() . Умножим (б) справа на
. Умножим (б) справа на ![]() и воспользуемся полученными выражениями
для
и воспользуемся полученными выражениями
для ![]() и
и ![]() :
:
![]() .
.
Получили, что ![]() - полиномиальная матрица. Таким образом,
- полиномиальная матрица. Таким образом, ![]() и
и ![]() -
полиномиальные матрицы. Следовательно,
-
полиномиальные матрицы. Следовательно, ![]() . Делаем заключение, что матрица
. Делаем заключение, что матрица ![]() унимодальная.
унимодальная.
S30. ![]()
![]()
![]() Пусть
для
Пусть
для ![]() дано правое взаимно простое
разложение
дано правое взаимно простое
разложение ![]() . Тогда существуют
матрицы
. Тогда существуют
матрицы ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() такие,
что
такие,
что
![]()
![]()
![]()
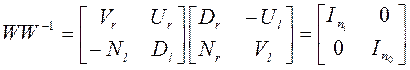 .
.
Здесь (![]() ) - левое взаимно простое разложение матрицы Н.
Это уравнение называют обобщенным тождеством Безу (generalized Bezout identity).
) - левое взаимно простое разложение матрицы Н.
Это уравнение называют обобщенным тождеством Безу (generalized Bezout identity).
Доказательство.
У пары ![]() найдем наибольший общий
правый делитель (S21):
найдем наибольший общий
правый делитель (S21):
![]()
![]()
![]()
![]()
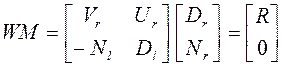 .
(а)
.
(а)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.