Полиномиальные матрицы. Унимодальность, левые/правые делители, элементарные операции, эквивалентность, Эрмитова форма, матричное полиномиальное разложение, тождество Безу, правильность, строчная/столбцовая степень, страница 2

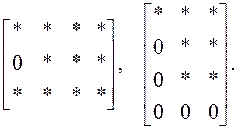
Подобную форму называют Эрмитовой строчной формой (Hermit row form).

$2.  Привести матрицу  к Эрмитовой строчной форме :

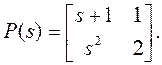
Найти соответствующую матрицу  такую, чтобы . (воспользоваться элементарными строчными операциями и понятием эквивалентности - S7, S10).

S14.  Пусть , т. е. матрица полного столбцового ранга (full column rank) над , т. е. . Это равносильно существованию унимодальной матрицы L такой, что 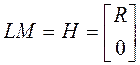, где R - верхнетреугольная невырожденная унимодальная матрица размером  и матрица 0 имеет размеры . Аналогично вводится понятие матрицы полного строчного ранга (full row rank). Попробуйте сделать это сами!

S15.  Эрмитовой столбцовой формой (Hermit column form) называется нижнетреугольная матрица:

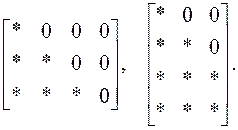
Произвольная матрица  может быть приведена к подобному виду (облзначим ее Н) посредством элементарных операций над столбцами, что соответствует умножению М справа на R: .

S16.  Используя элементарные строчные и столбцовые операции, приведенные в S7, S13, S15, произвольную матрицу М можно преобразовать к диагональному виду:

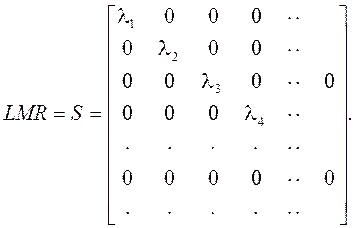
Унимодальные матрицы L и R соответствуют элементарным строчным и столбцовым операциям. Такую форму называют формой Смита (Smith form). Ненулевой блок матрицы S содержит инвариантные полиномы  матрицы М (invariant polynomials), обладающие свойством  - “полином  делит полином ”. Обычно полиномы  нормированы (monic polynomial) - коэффициенты при старших степенях равны единице.

$3.  Рассмотрим пример приведения матрицы к форме Смита:

 ~  ~  ~  ~ .

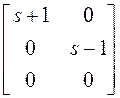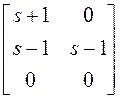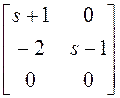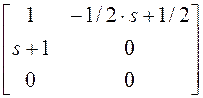Знак “~”, стоящий между двумя матрицами А ~ В, обозначает эквивалентность матриц (equivalence), т. е. что существуют унимодальные матрицы L и R такие, что . Эти прелбразования соответствуют операциям: второй столбик прибавляем к первому столбику, первую строку вычитаем из второй строки, меняем местами первую и вторую строки, умножаем первую строку на -1/2. Если теперь умножить первую строку на  и прибавить ко второй строке, а после этогопервый столбик умножить на  и прибавить ко второму, получим искомую форму

~  ~ .

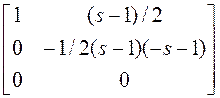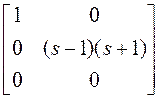Матрицу М(s) попробуйте привести к форме Смита:

.

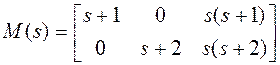S17.  Следующие утверждения эквивалентны:

1)  M эквивалентна N;

2)  M и N имеют одну и ту же форму Смита;

3)  M и N имеют одни и те же ивариантные полиномы;

4)  M и N имеют одни и те же детерминантные делители.

Нормированный наибольший общий делитель  всех  миноров матрицы М называется детерминантным делителем (determinantal divisor).

S18.  Размерность пространства X решений  уравнения , где ,  - нулевой столбец размером ,  - невырожденная, равна степени определителя матрицы :

.

S19.  Базисные элементы  (векторы размерности n) пространства решений  (S18,  - невырожденная) позволяют установить взаимно однозначное соответствие (linear bijection или isomorphism) между  и : для всякого  существует единственный вектор  из  такой, что , где . Вектор  называют вектором состояния (vector state).

S20.  При переходе от одного полиномиального матричного описания

(кратко ) посредством унимодальных преобразований

к другому

получаем . Здесь  - унимодальные матрицы.

S21.  Рассмотрим процедуру поиска наибольшего общего правого делителя (greatest common right divisor) для матриц  и , где - число входов, - число выходов. Составим матрицу 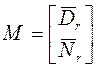. Посредством строчных операций, что соответствует умножению М слева на унимодальную матрицу W, приведем ее к верхнетреугольному виду:

.

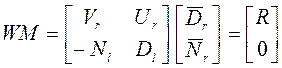Здесь матрица R имеет верхнетреугольный вид, а матрица W разбита на блоки в соответствии с размерами R ( и  - квадратные).