Полиномиальные матрицы. Унимодальность, левые/правые делители, элементарные операции, эквивалентность, Эрмитова форма, матричное полиномиальное разложение, тождество Безу, правильность, строчная/столбцовая степень, страница 4

Здесь  - наибольший общий правый делитель матриц  и матрица W - унимодальная. В нашем случае  - унимодальная. В последней формуле можем считать, что . В противном случае необходимо осуществить элементарные строчные операции над (а), соответствующие матрице :

.

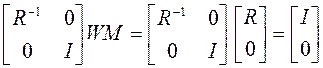Тогда (а) преобразуется в , где .

Так как () - левое взаимно простое разложение, то существуют матрицы ,  (S28) такие, что , что равносильно

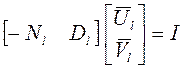                                                          .                                                  (б)

“Объединим” два уравнения (а) и (б):

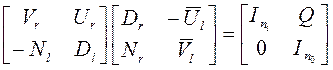                                           .                                      (в)

Получили “лишнее” уравнение . Умножим справа уравнение (в) на матрицу

, что соответствует элементарным операциям над столбцами, так как эта матрица унимодальна. Из (в) получаем:

.

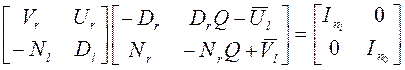Если обозначить , , получим искомое соотношение .

S31.  Утверждается, что для  ранга r () существуют унимодальные матрицы  такие, что , где матрица , называемая формой Смита-Макмиллана (Smith-McMillan form), она имеет вид

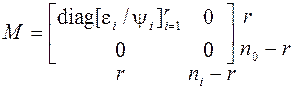                                               .                                        (а)

Здесь  - нормированные взаимно простые полиномы такие, что , ,  - нормированный наименьший общий делитель всех знаменателей элементов матрицы М.

Доказательство.Находим нормированный наименьший общий знаменатель (least common denominator) d всех элементов матрицы , что позволяет вычислить матрицу , , откуда

                                                                  .                                                              (б)

Далее находим форму Смита S для N (S16): , где

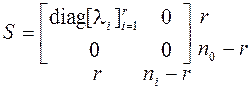                                                  .                                             (в)

Размеры блоков здесь такие же, как и у матрицы М, так как . Полиномы  обладают свойством . Матрицы L, R - унимодальные. Из (б) получаем

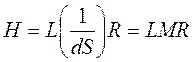, где

.

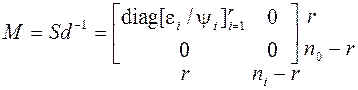Элементы ненулевого диагонального блока  матрицы М получены из  (в) в результате сокращения

                                                              =                                                           (г)

и являются нормированными взаимно простыми полиномами. Осталось показать, что , , . Но  (т. е.  делит  без остатка), и с учетом (г) можем записать

.

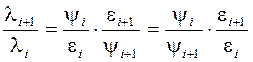И так как ,  - взаимно простые, то из последнего соотношения получаем, что , .

S32.  Рассмотрим процедуру поиска полиномиального матричного взаимно простого разложения для матрицы Н. Обозначим

, ,

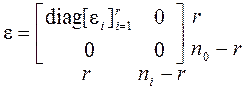(а)

.

Тогда  и, учитывая, что , получим:

                           .                      (б)

Использовали обозначения (L, M - унимодальные):

                                      .                                 (в)

В формуле (б) получены правое и левое полиномиальные разложения матрицы Н. Осталось показать, что это взаимно простые разложения. Найдем ранг матрицы :

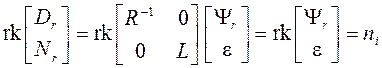, откуда следует (S24), что матрицы - взаимно простые.

Процедура поиска разложения следующая:

1)  находим форму Смита-Макмиллана (S31). “Элементарные” операции позволяют найти матрицы L, R;

2)  находим матрицы ;

3)  по формулам (в) вычисляем матрицы разложения.

$8.  Объяснить размеры матриц в формуле (а) из S32.

S33.  Пусть . “Числитель” разложения Н эквивалентен любой из форм  ~ e ~ , (формулы (а), (в) из S32). Индексы обычно не пишут.

“Знаменатели” разложения () имеют одни и те же инвариантные полиномы, и они эквивалентны, если .

S34.  Пусть . Рассмотрим предел

.

Последнее включение обозначает, что все элементы матрицы  - комплексные числа (это конечные числа! Обычно считают, что , и если необходимо оперировать с , то вводят множество ). Такие матрицы Н называют правильными (proper) и обозначают .