






Лапласа), распространенные на многоканальные/многомерные системы, существенно богаче и иногда несколько сложнее. По каким-то причинам не только в научной, но и в учебной литературе на русском языке это направление, несмотря на его большую “ инженерную прозрачность” (по сравнению с методами пространства состояний), не нашло должного отражения. В связи с отсутствием учебной литературы по этому направлению и в связи с тем, что на кафедре автоматики Новосибирского государственного технического университета давно ведутся исследовательские работы в этом направлении, а также имеется опыт в изложении данного материала студентам, было решено написать пособие.
Пособие написано так, чтобы помочь заинтересованному читателю войти в проблематику синтеза многомерных систем с использованием матричных передаточных функций и связанных с ними полиномиальных описаний. Не все термины имеют соответствующий русский эквивалент, поэтому они даются в английском написании, что позволит читателю подготовиться к работе с литературой на английском языке. Список из более, чем сотни терминов приведен в конце пособия. Ввиду малого объема пособия изложение дается сжатым и представляет в некотором смысле справочную информацию. Различные понятия, определения, свойства и утверждения имеют единую нумерацию: S1, S2, и т.д., что должно облегчить чтение. Для самоконтроля понимания материала вставлено большое количество вопросов различной степени сложности – легкие вопросы помечены $; и сложные $$.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
![]() - комплексная переменная;
- комплексная переменная;
![]() - комплексные числа;
- комплексные числа;
![]() - правая (левая) полуплоскость комплексной плоскости;
- правая (левая) полуплоскость комплексной плоскости;
t - транспонирование;
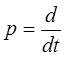 - оператор дифференцирования;
- оператор дифференцирования;
![]() -
вещественные числа;
-
вещественные числа;
![]() - множество векторов размерности n
из вещественных чисел;
- множество векторов размерности n
из вещественных чисел;
![]() - множество матриц размером
- множество матриц размером ![]() из вещественных чисел;
из вещественных чисел;
![]() - знак принадлежности (например,
- знак принадлежности (например, ![]() );
);
![]() - единичная матрица (иногда указывают размеры -
- единичная матрица (иногда указывают размеры - ![]() );
);
![]()
![]()
![]()
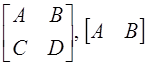 -
блочные матрицы;
-
блочные матрицы;
![]() - множество полиномов (передаточных функций);
- множество полиномов (передаточных функций);
![]() - множество (строго) правильных передаточных
функций;
- множество (строго) правильных передаточных
функций;
![]() - полиномиальные матрицы (матричные передаточные функции);
- полиномиальные матрицы (матричные передаточные функции);
![]() - произведение матриц А и В;
- произведение матриц А и В;
![]() - наименьшее из а и b;
- наименьшее из а и b;
![]() - диагональная матрица (например,
- диагональная матрица (например, ![]() );
);
![]() - предел (например,
- предел (например, ![]() );
);
![]() - производные переменной x
по t;
- производные переменной x
по t;
![]() -
степень полинома
-
степень полинома ![]() (степень столбца i или строки j матрицы
(степень столбца i или строки j матрицы ![]() );
);
![]() -
“для всякого” (например,
-
“для всякого” (например, ![]() (i - целое)
(i - целое) ![]() - четное);
- четное);
![]() -
“существует” (например,
-
“существует” (например, ![]() (i - целое) такое, что
(i - целое) такое, что ![]() );
);
![]() -
“существует единственный”;
-
“существует единственный”;
![]() - читается “следует” (например,
- читается “следует” (например, ![]() (из А следует В));
(из А следует В));
![]() - например,
- например, ![]() (утверждение А следует из
утверждения В);
(утверждение А следует из
утверждения В);
![]() - “тогда и только тогда” (“if and only if” или
“iff”);
- “тогда и только тогда” (“if and only if” или
“iff”);
![]() - знак определения (например,
- знак определения (например, ![]() );
);
![]() - определитель матрицы М;
- определитель матрицы М;
![]() - матрица, обратная матрице М;
- матрица, обратная матрице М;
![]() -
например,
-
например, ![]() равносильно
равносильно ![]() , где
, где ![]() и
и ![]() ;
;
![]() -
матрица А имеет соответствующие размеры;
-
матрица А имеет соответствующие размеры;
![]() ~В
- эквивалентные матрицы;
~В
- эквивалентные матрицы;
![]() -
присоединенная матрица (
-
присоединенная матрица (![]() );
);
![]() -
знак включения (например,
-
знак включения (например, ![]() ).
).
1. ВВЕДЕНИЕ
Одномерные/одноканальные системы, многомерные / многоканальные системы, матричные передаточные функции, матричное полиномиальное описание, псевдовектор состояния, левое/правое матричное разложение, системная матрица.
Поясняется смысл матричной передаточной функции на конкретном примере, и происходит знакомство читателя с такими возможными описаниями систем управления, как полиномиальные матрицы, полиномиальное матричное представление, системная матрица.
За последние годы вышло колоссальное количество работ по проектированию систем управления взаимосвязанными процессами и объектами. Их можно разбить на две группы: синтез в пространстве состояний и синтез в частотной области (в изображениях). Несмотря на увлечение методами пространства состояний, внимание к частотным методам не ослабевало и даже увеличилось. Это, по-видимому, связано с тем, что частотный метод более привычен для инженеров и возможности его ничуть не уже, чем у методов, основывающихся на пространстве состояний. В сказанном можно убедиться по многочисленным публикациям.
Преобладающая часть работ в этом направлении написана на английском языке. Здесь можно указать большое количество работ авторов, внесших значительный вклад в развитие частотных методов синтеза для многоканальных (многомерных) систем. И надо или ссылаться на всех, так как они все достойны этого
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.