Стабилизация двухмассовой системы: модальный метод синтеза в пространстве состояний

СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. – 2010. – № 1(59). – 21–31

УДК 681.513

СТАБИЛИЗАЦИЯ ДВУХМАССОВОЙ СИСТЕМЫ: модальный МЕТОД СИНТЕЗА в пространстве состояний

А.А. Воевода©, Е.В. ШОБА§

На примере двухканальной системы продемонстрирован модальный метод синтеза в пространстве состояний с использованием пропорциональной матрицы в канале обратной связи. Для оценки вектора состояния использован наблюдатель полного порядка.

Ключевые слова: многоканальная система, двухмассовая система, синтез, модальный метод, пространство состояний, наблюдатель, обратная связь.

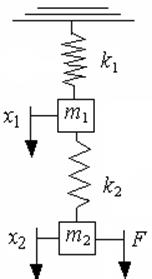
               Постановка задачи. В качестве объекта управления возьмем двухмассовую систему (рис.1), в которой два управляющих сигнала, силы  и , приложены к массам  и , подвешенных последовательно на двух пружинах жесткости k₁ и k₂,  а регулируемые величины – положение грузиков  и . В отличие от [1, 2], где рассмотрен модальный метод синтеза одноканальной и двухканальной системы с использованием полиномиального представления, ниже приведен расчет классическим способом с использованием пространства состояний.

При доступности вектора состояния  объекта

,                                                                   (1)

для смещения полюсов объект охватывают обратной связью , где - матрица коэффициентов. Тогда уравнение системы следующее: . Выбором можно задать полюса системы. Удобно эти вычисления производить в управляемой канонической форме.

Если вектор состояния не доступен, то необходимо ввести наблюдатель, например, полного порядка:

.                                                         (2)

Матрица  вычисляется из условия быстрого, по сравнению с переходными процессами в системе, затухания. Ошибка оценки  вектора состояния  описывается уравнением . Вычисление  удобно производить в наблюдаемой канонической форме. В этом случае матрица  «подключается» к оценке :

.                                                                                   (3)

Расчеты по определению матриц  и  удобно производить по отдельности, так как характеристическое уравнение всей системы определяется так: ×.

Решим задачу автономизации каналов. Проведем расчет двухканального регулятора, обеспечивающего заданные полюса замкнутой системы, в три этапа:

1) в предположении доступности вектора состояния рассчитаем обратную связь (коэффициентная матрица) в канонической управляемой форме;

2) вычислим наблюдатель вектора состояния полного порядка в канонической наблюдаемой форме;

3) перейдем к единому базису.

Модель объекта.

В предположении отсутствия демпфирования модель объекта «вход - выход» следующая:

,             (4)

.

Объект – это двухканальная система, между входами и выходами которой находятся по два интегратора. Очевиден переход к описанию в пространстве состояний - достаточно выходы интеграторов обозначать справа налево: - у канала «первый вход – первый выход», - у канала «второй вход

– второй выход».

Рис.1. Модель объекта         Получили управляемую каноническую форму:  

,

,             (5а)

,

,

,       .                                                   (5б)

Если выходы интеграторов обозначать слева на право, то получим наблюдаемую каноническую форму:

,  

,                                                                         (6а)

,

,

,       .                                                 (6б)

Зададим следующие значения параметров объекта: .

Вычисление матрицы обратной связи.  В матричном виде уравнения (5) запишутся так:

,    .                               (7)

Воспользовавшись (5) найдем матрицы , соответствующие управляемой канонической форме:

, , .

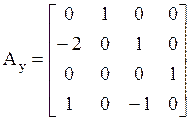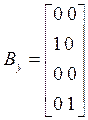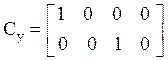Матрица состоит из четырех матриц размером 2 на 2 -  (j, k=1, 2): диагональные матрицы описывают собственные свойства первого и второго каналов, а недиагональные матрицы не нулевые и указывают на перекрестные связи между каналами. Таким образом, введением матрицы  в обратную связь

, 

в предположении доступности вектора состояний , необходимо скомпенсировать элементы  матрицы  для устранения перекрестных связей. Собственные свойства канала «первый вход – первый выход» определяются коэффициентами второй строки матрицы : {-2 0}, что соответствует коэффициентам характеристического полинома . Собственные свойства канала «второй вход – второй выход» определяются коэффициентами второй строки матрицы : {-1 0}, что соответствует коэффициентам характеристического полинома . Зададим собственные свойства каналов системы полиномом , что соответствует полюсам -1, -1. Таким образом, матрицу  находим из условия:

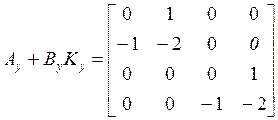.                               (8а)

Матрица неизвестная – элементы ее обозначим :

.

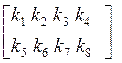Вычислим :

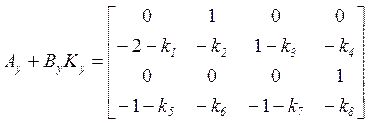          (8б)

Из сравнения (5а) и (5б) находим элементы матрицы :

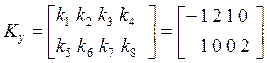.                                   (9)

Здесь число уравнений равно числу неизвестных. Выполним проверку, а именно, найдем передаточную функцию объекта по формуле :

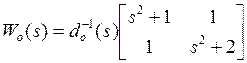, где , и передаточную функцию объекта, охваченного обратной связью  по состоянию :

.

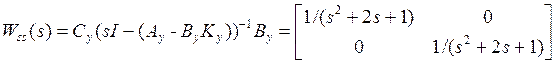Вычисление наблюдателя полного порядка.  Запишем уравнения (6) в матричном виде:

,    .                                 (10)

Здесь

,  ,  .

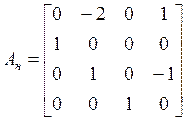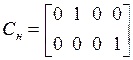Очевидно, что мы получили наблюдаемую каноническую форму. Матрицы ,  и  составлены из матриц размером 2×2. Матрица состоит из четырех матриц  размером 2×2: диагональные матрицы описывают собственные свойства первого и второго каналов: Собственные свойства канала «первый вход – первый выход» определяются коэффициентами