










СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. – 2010. – № 3(61). – 25–34
УДК 681.513
О РАЗРЕШИМОСТИ ЗАДАЧИ АВТОНОМИЗАЦИИ
МНОГОКАНАЛЬНОЙ СИСТЕМЫ* ч.2
А.А. Воевода, Е.В. ШОБА
При некоторых соотношениях параметров многоканальной системы задача автономизации становится неразрешимой. Подобного рода особенности многоканальных систем рассмотрены на примере двухканальной системы, состоящей из трех масс, соединенных упругими звеньями.
Ключевые слова: многоканальная система, трехмассовая система, синтез, полиномиальное разложение, автономизация, желаемая характеристическая полиномиальная матрица.
Задача синтеза линейной многоканальной системы методом разложения на полиномиальные матрицы и решения диофантова уравнения, на примере трехмассовой системы с двумя управляемыми сигналами и двумя регулирующими воздействиями (два входа – два выхода), рассмотрена в [1], где получено описание в виде левого и правого полиномиального матричного разложения. Данная работа продолжает исследования, начатые в [2-5], и базирующиеся на [6].
5. СИНТЕЗ РЕГУЛЯТОРА: РЕШЕНИЕ ДИОФАНТОВА УРАВНЕНИЯ
Запишем диофантово уравнение в матричном виде:
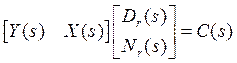 , (1)
, (1)
где
![]() ,
,![]() , (2)
, (2)
Выпишем матрицы ![]() и
и ![]() [1]:
[1]:
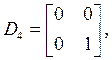
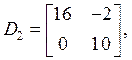
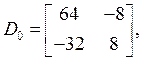 (3)
(3)
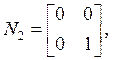
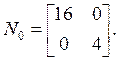
Вспомним, что размеры всех матриц 2![]() 2 и развернем (1):
2 и развернем (1):
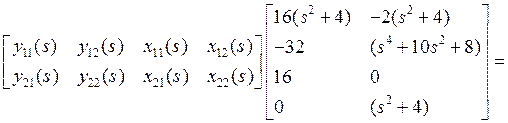
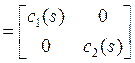 .
(4)
.
(4)
Матрицу ![]() выбрали
диагональной. Рассмотрим вопрос выбора степеней полиномов
выбрали
диагональной. Рассмотрим вопрос выбора степеней полиномов ![]() ,
, ![]() и
и ![]() .
.
5.1. Начнем с выбора степеней ![]() - ограничимся степенью 4-е
- ограничимся степенью 4-е ![]() в предположении, что регулятор правильный.
Из рассмотрения выше приведенного матричного уравнения (4) очевидно, что
в предположении, что регулятор правильный.
Из рассмотрения выше приведенного матричного уравнения (4) очевидно, что
![]() .
.
Для правильности матричной
передаточной функции регулятора ![]() , заданного правым
взаимно простым полиномиальным разложением в предположении, что матрица
, заданного правым
взаимно простым полиномиальным разложением в предположении, что матрица ![]() столбцово-приведенная (степень
определителя ее равна сумме столбцовых степеней) необходимо и достаточно, чтобы
столбцовые степени матрицы “числителя” регулятора были не больше столбцовых
степеней “знаменателя” регулятора:
столбцово-приведенная (степень
определителя ее равна сумме столбцовых степеней) необходимо и достаточно, чтобы
столбцовые степени матрицы “числителя” регулятора были не больше столбцовых
степеней “знаменателя” регулятора:
![]() .
.
Таким образом, очевидно, что необходимо выполнить условия:
![]() .
.
При сделанных предположениях после подстановки матричных полиномов в уравнение (4) и приравнивания коэффициентов при одинаковых степенях получим 7-мь матричных уравнений с 6-ью матричными неизвестными. Данная система почти всегда не имеет решения.
5.2. Повысим степени
полиномов ![]() : пусть
: пусть ![]() .
Проводя анализ подобно выше приведенному получим:
.
Проводя анализ подобно выше приведенному получим:
![]() ,
,
![]() .
.
Можем выписать “структуру” матриц ![]() и
и ![]() :
:
![]()
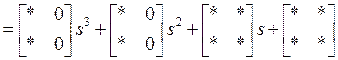 , (5)
, (5)
![]()
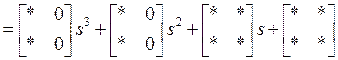 , (6)
, (6)
где звездочками помечены элементы, подлежащие определению.
Подставим ![]() ,
, ![]() ,
, ![]() ,
, ![]() из (2), (3), (5) в (1):
из (2), (3), (5) в (1):
![]()
![]()
![]() .
.
Приравняв коэффициенты при ![]() с одинаковыми степенями в левой и правой
части получим систему линейных уравнений, которую можно записать в матричном
виде
с одинаковыми степенями в левой и правой
части получим систему линейных уравнений, которую можно записать в матричном
виде
![]() .
(7)
.
(7)
Здесь:
![]() ,
, ![]() ,
,
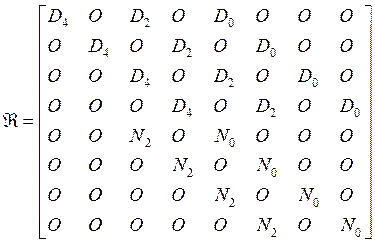 . (8)
. (8)
Получили систему матричных уравнений с
8-ью матричными неизвестными и восемью матричными уравнениями. Подставим
значения ![]() ,
, ![]() из (3)
в (8):
из (3)
в (8):
![]()
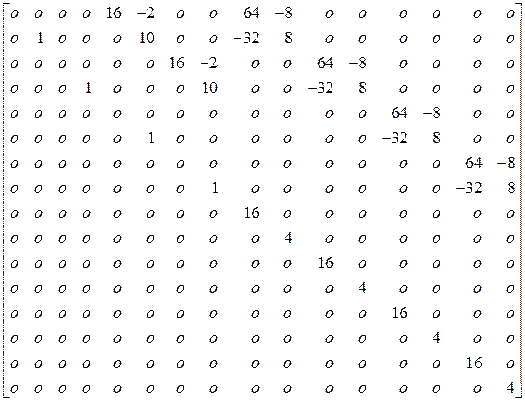 .
.
Учтем структуру регулятора, а именно,
что вторые столбики матриц ![]() ,
, ![]() ,
, ![]() ,
, ![]() - нулевые (5), (6). Это соответствует
нулевым значениям столбиков 2, 4, 10, 12 матрицы
- нулевые (5), (6). Это соответствует
нулевым значениям столбиков 2, 4, 10, 12 матрицы ![]() :
:
![]()
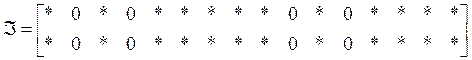 .
.
При умножении ![]() на
на
![]() строки 2, 4, 10, 12 матрицы
строки 2, 4, 10, 12 матрицы ![]() не играют роли и их можно выбросить вместе
со столбцами 2, 4, 10, 12 матриц
не играют роли и их можно выбросить вместе
со столбцами 2, 4, 10, 12 матриц ![]() . После этого столбцы 1,
2, 3, 4 матрицы
. После этого столбцы 1,
2, 3, 4 матрицы ![]() оказываются нулевыми.
Следовательно, столбцы 1, 2, 3, 4 матрицы
оказываются нулевыми.
Следовательно, столбцы 1, 2, 3, 4 матрицы ![]() обязаны
быть нулевыми – это ограничение на выбор матрицы
обязаны
быть нулевыми – это ограничение на выбор матрицы ![]() . В итоге
мы обязаны выбросить из
. В итоге
мы обязаны выбросить из ![]() и из
и из ![]() столбцы 1, 2, 3, 4. Матрицу
столбцы 1, 2, 3, 4. Матрицу ![]() после выбрасывания столбцов 2, 4, 10, 12
обозначим через
после выбрасывания столбцов 2, 4, 10, 12
обозначим через ![]() :
:
![]()
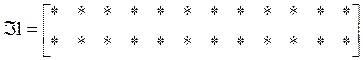 ,
,
![]()
![]()
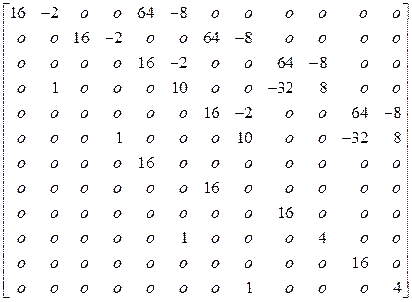
![]() .
.
Матрицу ![]() после
выбрасывания строк 2, 4, 10, 12 и столбцов 1, 2, 3, 4 обозначили через
после
выбрасывания строк 2, 4, 10, 12 и столбцов 1, 2, 3, 4 обозначили через ![]() . Матрицу
. Матрицу ![]() после
выбрасывания столбцов 1, 2, 3, 4 обозначим через
после
выбрасывания столбцов 1, 2, 3, 4 обозначим через ![]() :
:
![]()
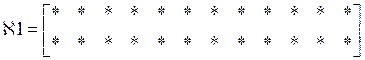 .
.
Получили систему уравнений ![]() . Проверим матрицу
. Проверим матрицу ![]() на
вырожденность -
на
вырожденность - ![]() . Нужно убрать две линейно
зависимые строки. По очереди убираем по одной строке из матрицы
. Нужно убрать две линейно
зависимые строки. По очереди убираем по одной строке из матрицы ![]() : при удалении строк 5, 7, 9, 11, 13, 14,
15, 16 (в исходной нумерации) ранг не понижается. Следовательно, строки нужно
убирать из этого набора. Теперь будем убирать по две строки в матрице
: при удалении строк 5, 7, 9, 11, 13, 14,
15, 16 (в исходной нумерации) ранг не понижается. Следовательно, строки нужно
убирать из этого набора. Теперь будем убирать по две строки в матрице ![]() из набора 5, 7, 9, 11, 13, 14, 15, 16. При
удалении строк 7 и 14 (нумерация строк сохранена из матрицы
из набора 5, 7, 9, 11, 13, 14, 15, 16. При
удалении строк 7 и 14 (нумерация строк сохранена из матрицы ![]() ) ранг остается равным 10. Следовательно,
строки 7 и 14 линейно зависят от остальных строк. В уравнении
) ранг остается равным 10. Следовательно,
строки 7 и 14 линейно зависят от остальных строк. В уравнении ![]() в матрице
в матрице ![]() им
соответствуют столбцы 7 и 14, т.е. первый столбик
им
соответствуют столбцы 7 и 14, т.е. первый столбик ![]() (обозначим
(обозначим
![]() ) и второй столбик
) и второй столбик ![]() (обозначим
(обозначим
![]() ). Левую часть
). Левую часть ![]() можем “расщепить”
на две части:
можем “расщепить”
на две части:
![]() . (9)
. (9)
Здесь:
![]()
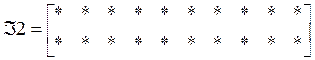 ,
,
![]()
![]()
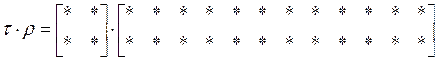
![]() ,
,
![]()
![]()
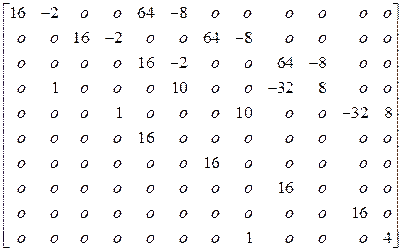 .
.![]()
![]()
![]()
![]()
Ранг матрицы ![]() десять
а столбцов 12 – найдем линейно зависимые
десять
а столбцов 12 – найдем линейно зависимые
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.