Программно-инструментальные средства для синтеза систем управления с аналоговыми и дискретными регуляторами

2. Программно-Инструментальные средства

для синтеза систем управления с аналоговыми и дискретными регуляторами

На основе данных, рассмотренных в первой главе, можно сделать вывод о том, что для большинства задач разработки систем автоматического управления достаточно использовать базовый комплект программно-инструментальных средств пакета ControlToolbox. При этом основой расчетов всех регуляторов являются модели объектов управления (ОУ), их частотные и временные характеристики. В комментариях к программам пакета для описания свойств систем управления непрерывного действия используется термин ContinuousTimeModels, а для дискретных систем – DiscreteTimeModels. С учетом специфики MATLAB версии 6 комментарии к приводимым ниже программным модулям выполнены строчными буквами.

2.1. Программная модель регуляторов

Функциональная схема системы с цифровым регулятором представлена рис. 2.1, на котором обозначены: входной задающий сигнал – V, управляющее воздействие – U, выходной контролируемый сигнал ОУ – Y. рассматриваться будут главным образом одноканальные объекты (SISO-SingleInputSingleOutput), для которых V, U, Y .

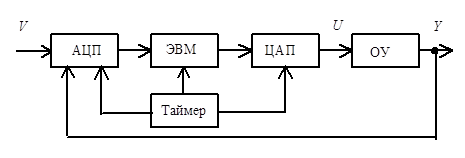
Рис. 2.1. Функциональная схема системы

В качестве решающего блока регулятора используется ЭВМ (микропроцессор, микроконтроллер). Назначение регулятора − формировать управление U, обеспечивающее заданное качество работы системы.

К аналого-цифровому (АЦП) и цифроаналоговому (ЦАП) преобразователям предъявляются требования синхронности и синфазности их работы. Таймер предназначен для синхронизации работы всей системы.

Требование синфазности обусловлено необходимостью использования Z-преобразования в расчетах. В реальных системах это условие выполняется приближенно. При точной синфазности на ЦАП будет передаваться управляющее воздействие, рассчитанное на предыдущем такте, вследствие чего возникнет дополнительная задержка на целый такт. Прежде чем запускать ЦАП, необходимо вычислить управляющее воздействие, поэтому алгоритм работы регулятора должен выглядеть в соответствии с рис. 2.2.

Рис. 2.2. Алгоритм работы регулятора

При этом в цепи обратной связи (ОС) возникает небольшая задержка, которой можно пренебречь. Фактически период дискретизации T распределяется между процессами согласно рис. 2.3.

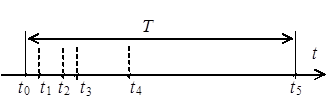
Рис. 2.3. Распределение времени дискретизации

Интервал  затрачивается на ожидание завершения работы АЦП;  − на расчет управляющего воздействия;  − на работу ЦАП;  − на расчет переменных состояния регулятора;  − на выполнение системных функций или ожидание следующего тактового импульса от таймера.

2.2. Модели и характеристики динамических звеньев

Математическая модель динамического объекта (звена) может быть представлена в нескольких формах: передаточная функция, пространство состояний, структурная схема, нули – полюса – коэффициент. Коэффициенты каждой модели задаются набором векторов или матриц. Кроме того, существует специальный класс LTI-объектов, который инкапсулирует стандартные операции и преобразования моделей (LTI – аббревиатура от LinearTimeInvariant – линейный или стационарный).

2.2.1. Передаточная функция

Передаточная функция (ПФ), как дробно-рациональная функция, записывается двумя полиномами: числителя и знаменателя в порядке убывания степеней. Так, для записи дискретной ПФ 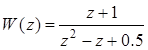 средствами MATLAB достаточно двух векторов: num=[1 1]; den=[1 -1 0.5];

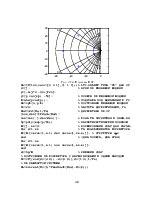
Используя подобное представление ПФ, можно выполнить построения временных и частотных характеристик:

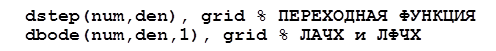
Результат выполнения показан на рис. 2.4.

Классическая запись ПФ (tf – TransferFunction) в виде двух полиномов вынуждает пользователя помнить, к какой именно ПФ они относятся. Упаковать больше информации о модели в одном месте позволяет использование LTI-объектов:

tf(num,den,1) % создание LTI-объекта из числителя и знаменателя

Результат создания LTI-объекта типа «tf» имеет вид:

Transfer function:

z + 1

-------------

z^2 - z + 0.5

Sampling time: 1

Представленный способ позволяет задавать как непрерывные, так и дискретные модели систем, а также передаточные матрицы для многоканальных систем.

2.2.2. Пространство состояний

Пространство состояний (ss – StateSpace) является гибким и универсальным способом описания динамических систем, обладающим к тому же свойствами компактности описания и малого накопления ошибок вычислений. Собственно описание задается четверкой матриц.

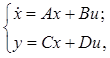     или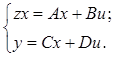    

Создание LTI-объекта из матриц пространства состояний выполняется строкой ss(A, B, C, D). Для создания дискретной модели нужно в списке аргументов указать пятый параметр – период дискретизации.

2.2.3. Множество нулей и полюсов

Этот способ задания удобно использовать в тех случаях, когда известны нули, полюсы и коэффициент ПФ (zpk – ZeroPoleGain). Например, для задания ПФ с нулями , полюсами  и единичным статическим коэффициентом достаточно записать:

zpk([-1 -10],[-0.1 -100],1).

2.2.4. Структурная схема