Решение. Пользуясь частотным подходом, можно сразу указать ПФ непрерывного корректирующего звена. Непрерывный фильтр содержал бы два нуля по –1 и два полюса по –10 в ПФ. Остается только найти соответствующий дискретный аналог.
Для применения модального подхода необходимо задать множество нулей и полюсов дискретного корректора. Их количество может быть таким же, как и у непрерывного корректора. Нули дискретного корректора задаются такими же, как полюсы дискретной ПФ объекта. Полюсы корректора задаются в окрестности центра круга устойчивости для повышения быстродействия.
На рис. 2.9 приведены частотные характеристики полученных систем (а – при частотном подходе; б – при модальном).
|
|
|
|
а б Рис. 2.9. Частотные характеристики |
|
Обсуждение результатов. Расширение полосы пропускания достигнуто в обоих случаях. Полученный с использованием частотного подхода корректор расширяет полосу пропускания системы, однако вносит большую неравномерность АЧХ (рис. 2.9, а). Модальный подход дает более ровную АЧХ (рис. 2.9, б).
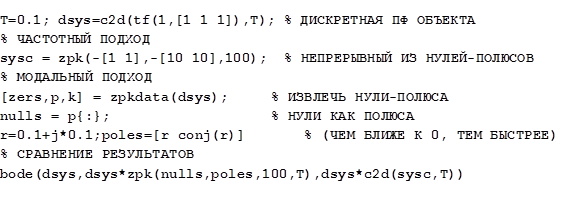
Попытка найти непрерывный эквивалент для полученного модальным способом корректора d2c(zpk(nulls,poles,100,T))дает неминимально-фазовое звено
Частотный метод расчета регуляторов не предназначен для расчета систем с такими звеньями. Указанные ограничения не уменьшают значимости подходов, наоборот, возможно, следует их комбинировать для получения более качественных результатов (см. sisotool).
Современная теория предлагает рассчитывать управляющее воздействие в функции не рассогласования, как классическая, а вектора состояния.
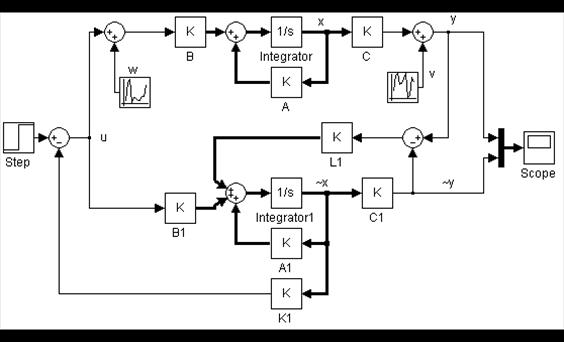
Рис. 2.10. Структурная схема системы с наблюдателем и регулятором
Расчеты оптимальных регуляторов (lqr, lqry, lqg) основаны на предположении, что вектор состояния объекта измеряется полностью или частично, а недостающие сигналы восстанавливаются наблюдателем или фильтром Калмана. Использование вектора состояния позволяет также рассчитывать систему с заданным расположением полюсов (place, acker). Если для расчета оптимального регулятора требуется решение уравнения Риккати, то для заданного расположения полюсов достаточно сформировать и решить систему линейных алгебраических уравнений (СЛАУ).
В случае если вектор состояния недоступен, расчет регулятора предваряется расчетом фильтра Калмана (kalman, kalmd). Структурная схема системы с наблюдателем и регулятором, набранная в Simulink, показана на рис. 2.10. После расчета наблюдатель и регулятор можно объединить в один блок и найти минимальную реализацию (рис. 2.11).
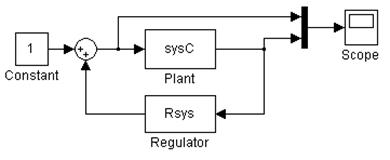
Рис. 2.11. Структурная схема минимальной реализации
Постановка задачи и исходные данные. ОУ характеризуется ПФ:
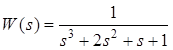 .
.
Вектор состояния не измеряется. Качество регулирования задается итегральной оценкой минимума энергии переходного процесса по выходу.
Решение. Все необходимые подпрограммы для расчета имеются в пакете control. Для решения достаточно составить головную программу и ввести исходные данные. Для нахождения регулятора, минимизирующего энергию переходного процесса на выходе, необходимо установить соответствующий весовой коэффициент больше остальных. Текст приведен ниже.

В результате расчета получится система с регулятором в цепи обратной связи. Для коррекции АЧХ (см. п. 2.6.1) или коэффициента передачи полученной замкнутой системы, возможно, потребуется включить в цепь задающего сигнала дополнительный блок. по-видимому, требуется расчет регулятора общего вида с двумя корректорами: в цепи обратной связи и в цепи задающего воздействия.
Еще один вариант расчета оптимального регулятора см. dcdemo.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.