Структурные схемы составляются графическим редактором Simulink с использованием блоков из его библиотеки. В библиотеке имеются блоки для задания передаточных функций, пространства состояний, нулей-полюсов-коэффициентов и LTI-объектов. Параметры блоков записываются в традиционном стиле MATLAB с помощью матриц, векторов или переменных из рабочего пространства. В [7] для представления описаний структурных схем, созданных в Simulink, введен термин «блок-диаграммы».
Иногда дискретную ПФ записывают с использованием отрицательных степеней z. Такой способ записи называют «цифровой фильтр». В этом случае следует воспользоваться командой: filt([1 1], [1 -1 0.5],1).
Результатом будет LTI-объект:
Transfer function:
1 + z^-1
-------------------
1 - z^-1 + 0.5 z^-2
Этому фильтру соответствует ПФ 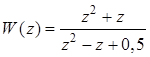 .
.
Вычислительное ядро MATLAB достаточно хорошо развито, чтобы пользователь мог самостоятельно за небольшое число шагов проделать непосредственные вычисления интересующих его характеристик. Вместе с тем имеется набор и специальных функций: bode(…) – диаграмма Боде (ЛАЧХ и ЛФЧХ), nyquist(…) – годограф Найквиста, step(…) – переходная функция, pzmap(…) – карта нулей и полюсов, sgridи zgrid – линии сетки и пр.
Пример 2.1. Требуется знать переходную функцию объекта, процесс в котором описывается уравнением АРСС
![]() .
.
Здесь необходимо циклически производить взвешенное суммирование нескольких последовательно взятых отсчетов. Если последовательно взятые значения x или y представить как вектор-столбец, то их перемещение можно осуществить с помощью матрицы сдвига вида
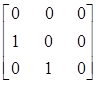
умножением вектора на эту матрицу. Окончательно алгоритм будет выглядеть так:

Пример 2.2. Требуется найти дискретную передаточную функцию для динамического звена
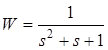 (2.1)
(2.1)
с фиксатором нулевого порядка, работающим на частоте 0,1 Гц.
Непосредственное вычисление основано на том, что решение соответствующего дифференциального уравнения записывается через матричную экспоненту [1].

Непосредственной подстановкой частоты можно получить АЧХ или ЛАЧХ, воспользовавшись известными соотношениями:
![]() ; (2.2)
; (2.2)
![]() ; (2.3)
; (2.3)
![]() .
.
Для построения АЧХ потребуются различные выражения в зависимости от способа задания модели динамического звена.
Пример 2.3.
Требуется определить модуль коэффициента передачи дискретного аналога для (2.1)
на частоте ![]() .
.

Использование LTI-объектов унифицирует использование математических преобразований над различными моделями динамических систем.
Пример 2.4. Требуется оценить влияние дискретизации по времени на частотные характеристики звена (2.1) из примера 2.2.
Ответ можно получить, если построить две диаграммы Боде в одних осях. Для этого достаточно перечислить все модели в списке параметров функции bode.
bode(lsys,dsys)
Результат представлен рис. 2.5.
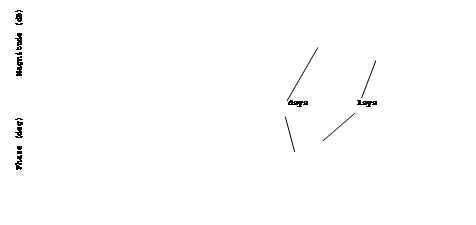
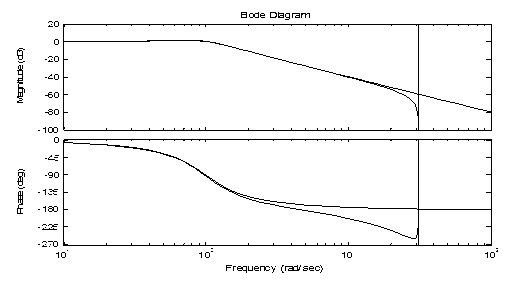
Рис. 2.5. Частотные характеристики звена 2.1 из примера 2.2
Вблизи частоты Найквиста (вертикальная линия на рис. 2.5) наблюдается сильное расхождение, которое в общем случае делает взаимно однозначное соответствие невозможным. Однако, используя различные методы дискретизации, можно приблизить частотные характеристики непрерывных и дискретных систем (см. notchdemo).
Все преобразования выполняются через промежуточное представление в пространстве состояний. Для быстрого ознакомления с преобразованиями из одной формы в другую см. ltidemo.
Для преобразования схемы, набранной с помощью Simulink, в LTI-объект используется функция linmod(…).
В результате серий преобразований могут появиться «лишние» переменные состояний или близких нулей и полюсов, которые можно было бы сократить. Эту задачу решает функция minreal(…). Избавиться от слишком больших или слишком малых коэффициентов в реализации модели позволяет функция balreal(…). Подробнее см. numdemo.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.