Программно-инструментальные средства для синтеза систем управления с аналоговыми и дискретными регуляторами, страница 3

Благодаря технологии LTI-объектов дискретные и непрерывные модели обрабатываются совершенно одинаково. Преобразования непрерывных систем в дискретные и обратно представлены соответственно функциями c2d(), d2c(), а также d2d() для изменения тактовой частоты.

Связь между параметрами преобразования Лапласа и Z-преобразования задается известным соотношением (2.3), но функция exp комплексного аргумента является периодической, поэтому взаимно однозначного соответствия между дискретными и непрерывными реализациями в общем случае не существует. Наглядное представление о преобразовании можно получить, воспользовавшись функциями построения линий сеток s-плоскости и z-плоскости. Область взаимно однозначного соответствия определяется на s-плоскости двумя горизонтальными линиями , где  − частота Найквиста (половина частоты дискретизации).

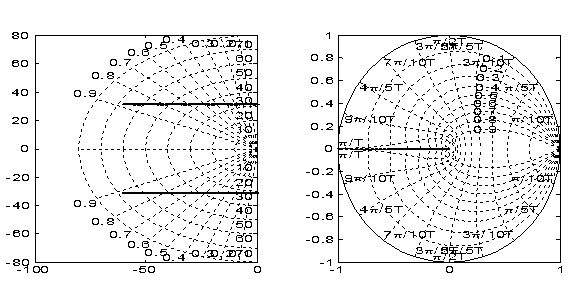
В результате получатся две диаграммы, представленные рис. 2.6 (а – изображена s-плоскость; б – изображена z-плоскость).

а                                                                               б

Рис. 2.6. Интерпретация преобразования  z= exp (sT)

Линии сетки удобно использовать при исследовании корневых портретов.

2.4. Устойчивость дискретных систем

Исследовать устойчивость можно по корневому портрету, его построение выполняет функция pzmap().

Области устойчивости непрерывных (левая полуплоскость) и дискретных (круг единичного радиуса) систем для полюсов различаются очень сильно (рис. 2.6). Однако частотные критерии устойчивости совпадают, хотя сами частотные характеристики различаются. Для визуализации частотных и временных характеристик можно просто перечислить интересующие модели как дискретные, так и непрерывные в одном списке при вызове соответствующих функций. Это было использовано в примере 2.3. Аналогичным образом можно построить годографы Найквиста (рис. 2.7):

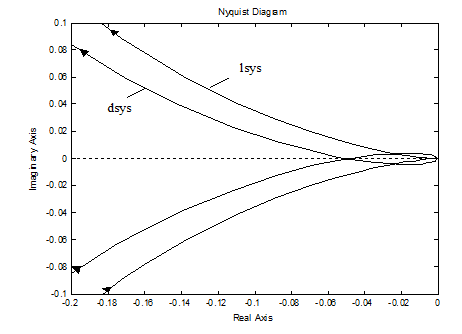
Рис. 2.7. Годографы Найквиста из примера 2.2

Сопоставляя годографы, можно отметить, что годограф дискретной модели захватывает третий квадрант, а непрерывной – нет.

2.5. Модели АЦП и ЦАП

В реальных системах внешний по отношению к микропроцессору сигнал перед обработкой превращается в цифровую форму посредством АЦП и обратно в аналоговую после обработки посредством ЦАП. На всем промежутке времени работы микропроцессора сигнал остается постоянным, такой способ преобразования называют фиксатором (экстраполятором) нулевого порядка (zero-orderhold). Микросхемы АЦП (ЦАП) характеризуются конечным диапазоном входных (выходных) напряжений и разрядностью. С учетом перечисленных особенностей модель АЦП (ЦАП) может быть собрана из библиотечных модулей Simulink так, как показано на рис. 2.8.

Рис. 2.8. Модель АЦП и ЦАП

Так, например, для 12-разрядного АЦП с диапазоном входных напряжений –5…+5 В параметры блоков следует установить следующим образом (табл. 1).

Таблица 1

Эти параметры устанавливаются средствами встроенного интерфейса каждого блока.

2.6. Примеры синтеза регуляторов

В расчетах регулятор (как устройство) заменяется эквивалентной дискретной моделью, которую для краткости также называют регулятором.

2.6.1. Расчет регулятора без обратной связи

Постановка задачи и исходные данные. Требуется рассчитать частотный корректор для объекта (2.1), выравнивающий спад АЧХ в высокочастотной области в пределах одной декады. Период дискретизации  Гц.

Предварительные замечания. Поставленную задачу можно решить несколькими способами. Наиболее известные – частотный и модальный. У каждого подхода есть ограничения и недостатки. Частотный подход позволяет оперировать с АЧХ непосредственно, но предназначен только для расчета устойчивых минимально-фазовых звеньев, ограничивая тем самым области расположения нулей и полюсов ПФ. Модальный подход имеет ограничение только на расположение полюсов ПФ, но не дает непосредственного представления об АЧХ. целесообразно использовать оба подхода и сравнить результаты.