Программно-инструментальные средства для синтеза систем управления с аналоговыми и дискретными регуляторами, страница 5

Постановка задачи и исходные данные. Задана ПФ объекта управления: 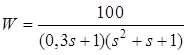; ЦАП и АЦП характеризуются следующими параметрами: 12 разрядов, шкала –5…0…+5 В. Частота выдачи управляющего воздействия – 20 Гц.

Замкнутая система должна иметь монотонный переходный процесс, соответствующий желаемой модели с передаточной функцией вида

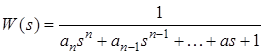
и временем окончания 0.5 с.

Решение. Для разработки программы предлагается выполнить следующие действия:

− рассчитать корректор;

− выполнить моделирование системы с учетом свойств ЦАП и АЦП;

− при необходимости выполнить масштабирование.

Выполнение каждого этапа предполагает проверку условий работы и при необходимости возврат к предыдущему этапу.

Расчет корректора, удовлетворяющего требованиям задания. Расчет является итерационной процедурой и выполняется в несколько шагов:

-  задается желаемая модель (уравнение переходного процесса);

-  находятся дискретные аналоги ПФ ОУ и желаемой модели;

-  формируется СЛАУ для расчета коэффициентов корректора по заданной желаемой ПФ;

-  решается СЛАУ и формируется корректор;

-  анализируется переходный процесс в замкнутой скорректированной системе (рис. 2.12).

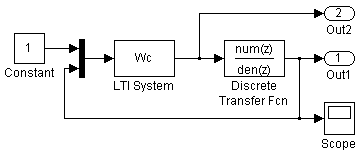
Рис. 2.12. Структура замкнутой цифровой системы

Для обеспечения заданного расположения полюсов замкнутой системы достаточно использовать корректор второго порядка вида «два полюса, два нуля». Порядок замкнутой системы в этом случае составит 5. Желаемая модель замкнутой системы соответственно должна быть 5-го порядка. Полюсы желаемой ПФ представлены на рис. 2.13. Расчет выполняется в системе MATLAB по программе, текст которой приведен ниже.

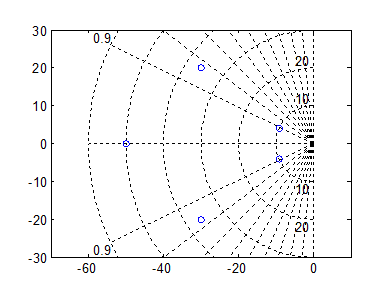
Рис. 2.13. Полюсы ПФ

Исследование качества полученного корректора выполняется по схеме рис. 2.14. Для сопряжения непрерывного объекта с цифровым регулятором в схему введен фиксатор нулевого порядка. Матрицы A, B, C, D регулятора получены преобразованием корректора, рассчитанного на предыдущем этапе.

При анализе качества необходимо обратить внимание на величины внутренних сигналов регулятора и соотнести их с возможностями управляющего микропроцессора. Так, для целочисленной 16-разрядной арифметики величины сигналов должны укладываться в диапазон представления целых чисел +32767…–32768, а выходной сигнал должен оставаться в диапазоне 12-разрядных чисел (+2047…–2048) для нормальной работы ЦАП.

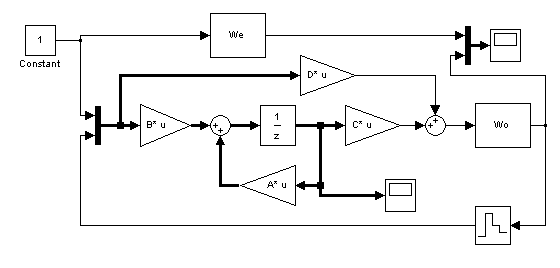
Рис. 2.14. Структурная схема проверки свойств корректора

Если система работает устойчиво, необходимо проверить работу с учетом свойств АЦП и ЦАП.

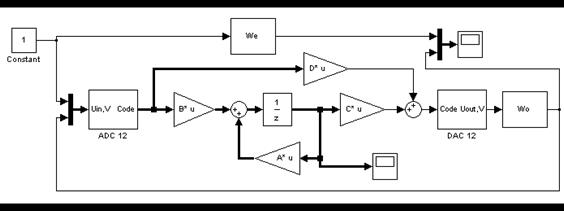
Рис. 2.15. Модель системы с учетом АЦП и ЦАП

Полученная модель системы (рис. 2.15) все еще использует плавающую арифметику, которая выполняется удручающе медленно на процессорах, где нет математического сопроцессора. Следующий этап тестирования будущего устройства – перевод всех вычислений на целочисленную арифметику или на арифметику с фиксированной точкой. Перевод переменных состояния в целые числа осуществляется двумя блоками: «Quantizer» и «Saturation» (рис. 2.16).

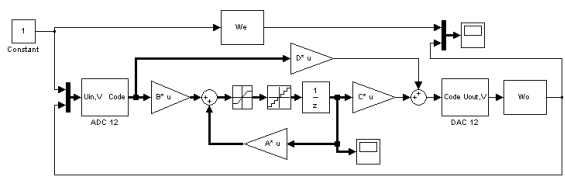Рис. 2.16. Модель системы с целочисленным вектором состояний

Если система все еще работает устойчиво, можно перевести и матрицы в целые числа. Сделать это нужно так, чтобы переменные состояния не достигали ограничения. Заключение о необходимости масштабирования делается на основе анализа полученных коэффициентов. В рассматриваемом примере коэффициенты матриц A и B меньше единицы, а C и D – больше. В этом случае можно A и B умножить на g = 2⁸ и округлить до целых, а переменные состояния поделить на g (рис. 2.17).

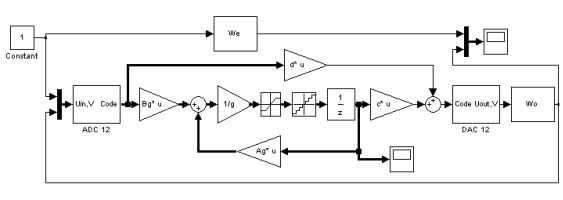
Рис. 2.17. Модель системы с фиксированной арифметикой

В программной реализации умножение и деление на 2ⁿ можно заменить сдвигами для увеличения быстродействия, а сдвиг на 8 разрядов вправо заменить отбрасыванием младшего байт результата. Окончательно программная реализация алгоритма управления будет выглядеть так:

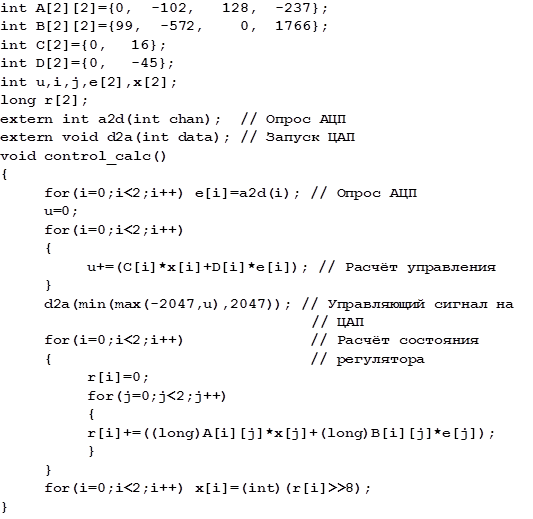
Представленные в данной главе программные модули могут быть использованы для решения широкого круга задач практического характера.