Организация, проведение и обработка результатов испытаний на основе положений пассивного эксперимента

       Министерство Образования  РФ

       НГТУ

       Кафедра Автоматики

Лабораторная работа № 6

«Организация, проведение и обработка результатов испытаний на основе положений пассивного эксперимента».

Факультет: АВТ                                       

Группа: АА-06

Студент:Беляев А. Н.                                    Преподаватель:

Кондратьев В.А.                                                                 

Дата сдачи:

Отметка о защите:

Новосибирск

2003г.

Цели работы: Исследовать методы проведения пассивного эксперимента, получить навыки обработки результатов и составление уравнения регрессии, а также построение автокорреляционных и взаимнокорреляционных функций.

Задачи:

1.  Расчет средних значений и дисперсий переменных;

2.  Построение автокорреляционных и взаимнокорреляционных функций;

3.  Получение уравнения регрессии.

Исходные данные:

1. количество факторов - 2;
2. количество выходных переменных - 2;
3. уровень значимости принятия гипотез  q = 0.05.
4. Размер фрагмента данных для анализа: 864 отсчетов.

Время моделирования составляет трое суток, значения факторов и выходных параметров снимается через каждые 5 минут.

Число переходов через среднее значение температуры дома – 57. Подсчет переходов осуществлен программно и представлен в Приложении1.

Все вычисления организованы в среде MathLab 5.3, листинг программы представлен в Приложении2.

Модель объекта испытаний представлена в Приложении3.

Представим в графическом виде данные, полученные при проведении пассивного эксперимента  на рис.1-3.

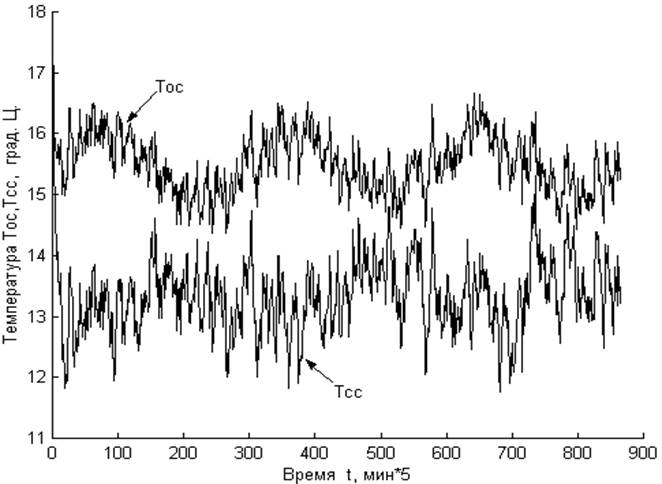
Рис.1 Входные факторы.

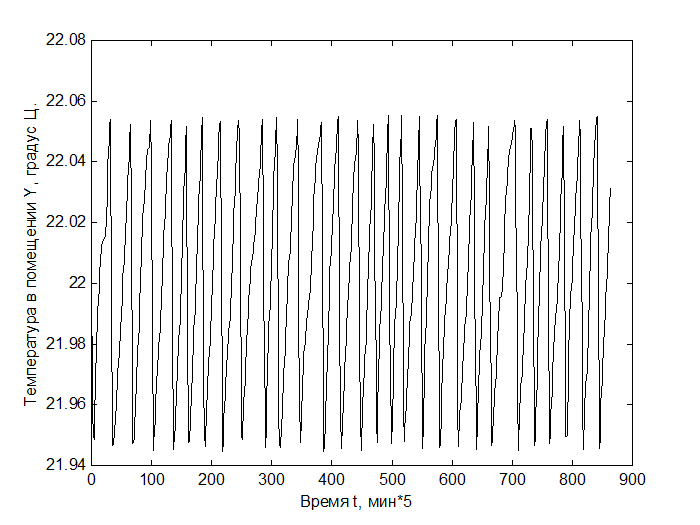
Рис.2 Температура в помещении

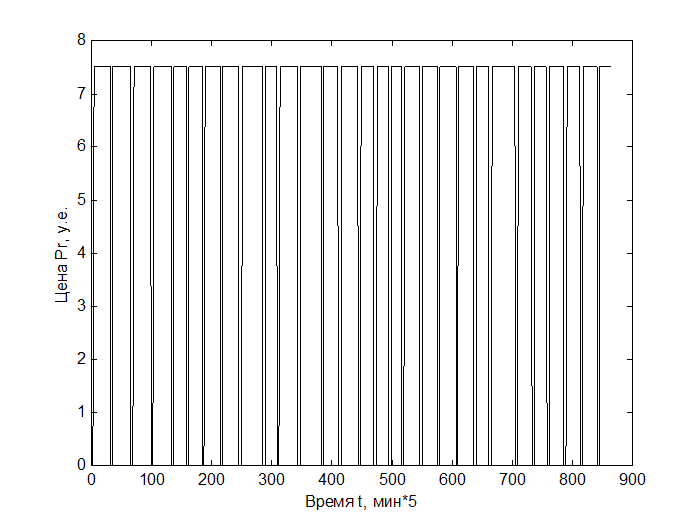
Рис.3 Цена за у.е. отопления

Величина интервала забора данных в обработку должна обеспечивать и некоррелированность факторов. Для непрерывных технологических процессов, для которых изменения переменных представляют собой некоторый случайный процесс, это проверяется по автокорреляционной функции входной переменной  R_xx по формуле:

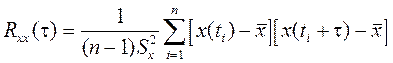
Автокорреляционные функции для обоих факторов представлены на рис.4-5

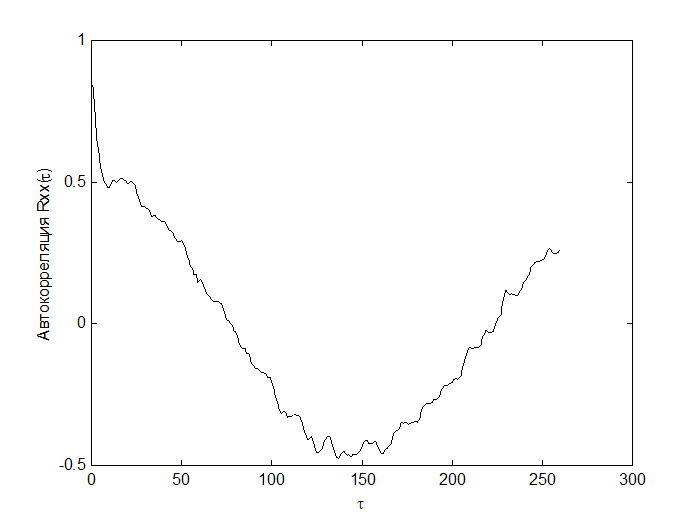
Рис.4 Автокорреляционная функция фактора окружающей среды.

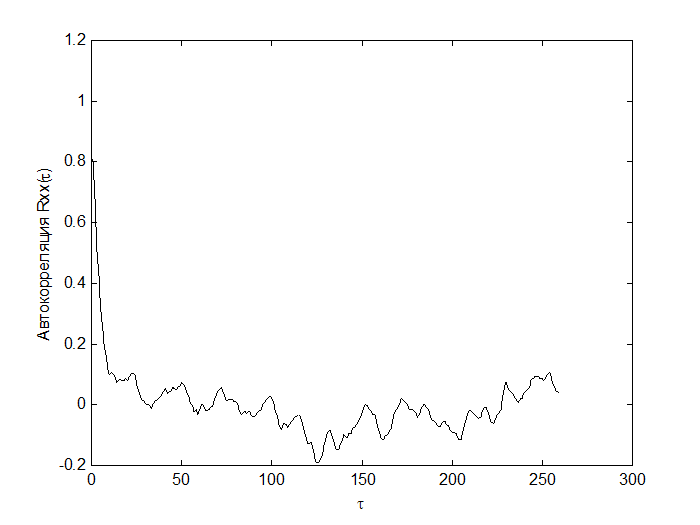
Рис.5 Автокорреляционная функция фактора социальной среды.

Для непрерывных технологических процессов важно знать, как изменяется теснота корреляционной связи между входными и выходными величинами в зависимости от временного сдвига t между ними. Выявить это можно, исследуя поведение взаимнокорреляционной функции:

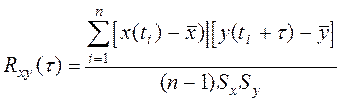
На рис. 6-7  изображёны графики взаимнокорреляционных функций.

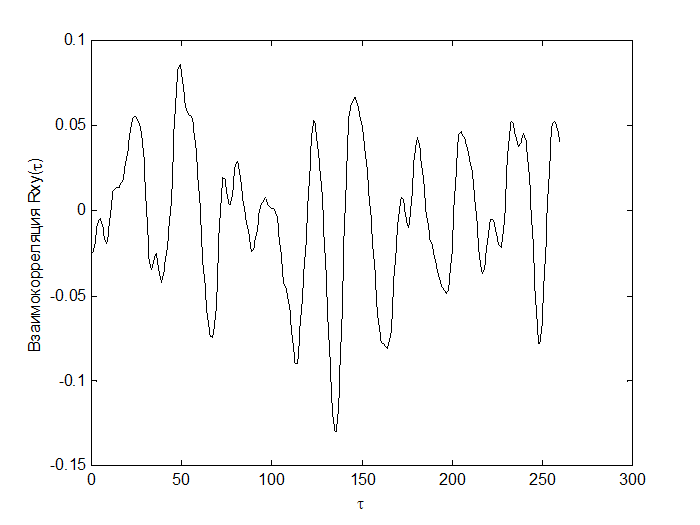
Рис.6 Взаимная корреляция между показаниями датчиков температуры дома и окружающей среды.

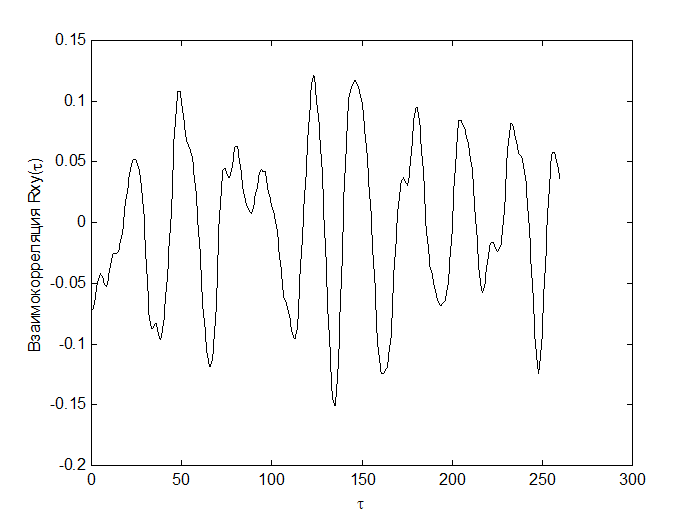
Рис.7 Взаимная корреляция между показаниями датчиков температуры дома и социальной среды.

Переход к нормированному представлению данных осуществляется с помощью следующих выражений:

;    

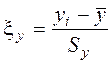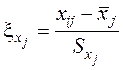
где Sx и Sy – вектора выборочных дисперсий матриц X и Y соответственно.

Коэффициенты уравнения регрессии определяются методом наименьших квадратов:

В результате расчетов получена следующая матрица коэффициентов уравнения регрессии

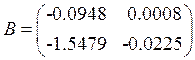
Следующим этапом работы является проверка значимости коэффициентов уравнения регрессии по ковариационной матрице с помощью критерия Стьюдента.

Значимость коэффициентов регрессии b_jвыявляется путем проверки гипотезы

, где  t_j и t_q,f - коэффициент и критерий Стьюдента

Коэффициент Стьюдента рассчитывается по формуле:

.

                       

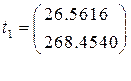
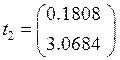
Критерий Стьюдента . 3 из 4  коэффициента регрессии являются статистически незначимыми, т.к. не подтверждается гипотеза .

Таким образом, первое уравнение регрессии равно нулю.

Следующим шагом проверим адекватность уравнений регрессии эксперименту с помощью критерия Фишера.

,                                                                     

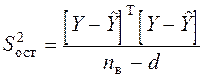где  n_в  - число наблюдений, взятых в обработку; d - число коэффициентов регрессии;

 - столбец расчетных значений

.    

Качество аппроксимации (адекватность уравнения регрессии эксперименту) можно оценить, проверив гипотезу

,                                                                    

где F - коэффициент Фишера

.       

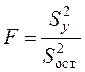Критическое значение критерия Фишера взято на уровне 1.2.