Чтение исходных данных, полученных при пассивном эксперименте. Формирование выборок зависимых и независимых переменных. Расчет средних значений и дисперсий для построения автокорреляционных и взаимно-корреляционных функций. Расчет и построение автокорреляционных функций для всех факторов по условию. Расчет и построение взаимно-корреляционных функций для всех выходных переменных и влияющих на них факторов

Методическая  демонстрашка От Сидоровой Е. 2001 г.

(приводится для возможностей MathCAD-7)

1. Чтение исходных данных, полученных при пассивном эксперименте.

Файл с данными пассивного эксперимента (например, data1) предварительно должен быть сформирован из общего массива, например, средствами Excel. Чтобы считать файл данных необходимо два раза щелкнуть на пиктограмме дискетки и в окрывшемся окне указать путь к нему.

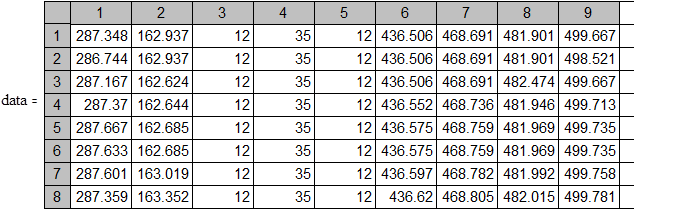
Необходимо задать (в соответствии с вариантом):

Количество факторов.

Количество выходных переменных

Уровень значимости принятия гипотез

1. Представление в графической форме всех приемлемых данных.

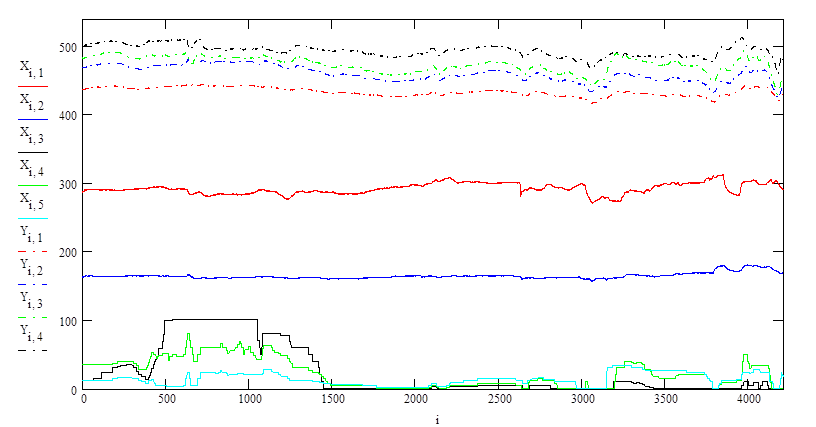
Рис. 1. Данные наблюдений, взятых в обработку

( X1 ... Xk - входные факторы; а Y1 ... Yl - выходные (зависимые) переменные)

2. Формирование выборок зависимых и независимых переменных.

Необходимо самостоятельно выбрать данные для дальнейшего исследования от А1 до А2 (рекомедутся брать не более 400 наблюдений, т. к. возможности Mathcad ограничены).

  

Х - матрица независимых переменных, а Y - зависимых.

 

n - число опытов

3. Расчет средних значений и дисперсий для постоения автокорреляционных и взаимнокорреля-ционных функций. Расчет производится для всех значений выборок с учетом сдвигов.

 

Определение числа используемых сдвигов.

    

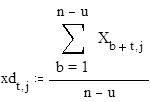
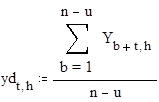
здесь xd и yd - матрицы средних значений для соответствующих зависимых и независимых переменных, а Sxd и Syd - матрицы выборочных дисперсий.

  

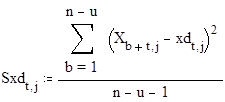
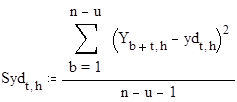
4. Расчет и построение автокорреляционных функций для всех факторов по условию

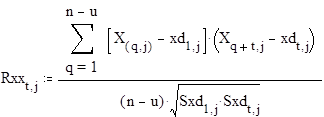
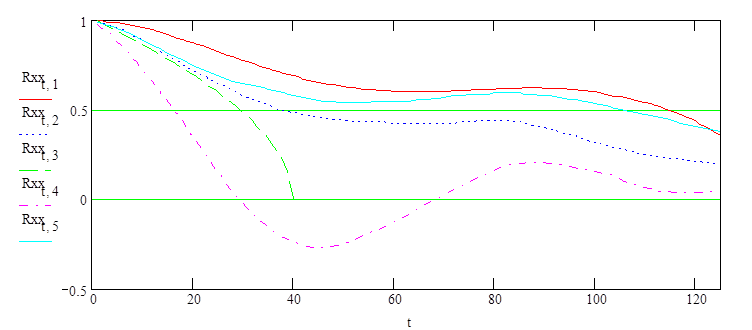
Рис.2. Графики автокорреляционных функций для входных факторов

5.   Расчет и построение взаимно-корреляционных функций для всех выходных переменных и влияющих на них факторов

-  для первой выходной переменной

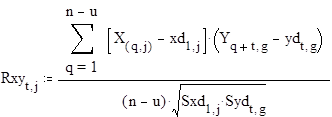
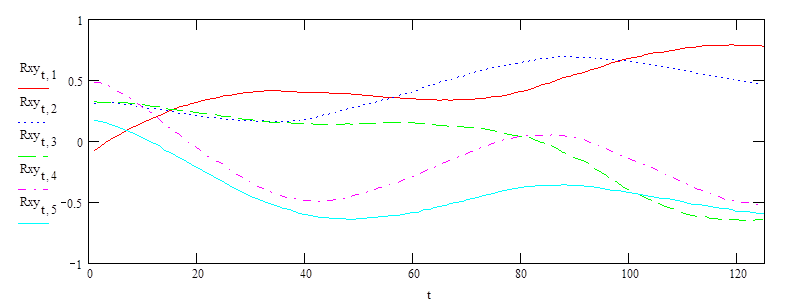
Рис. 3. Взаимно-корреляционные функции для первого выходного параметра

-  для второй выходной переменной

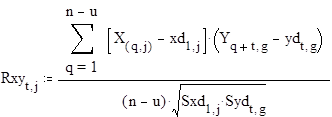
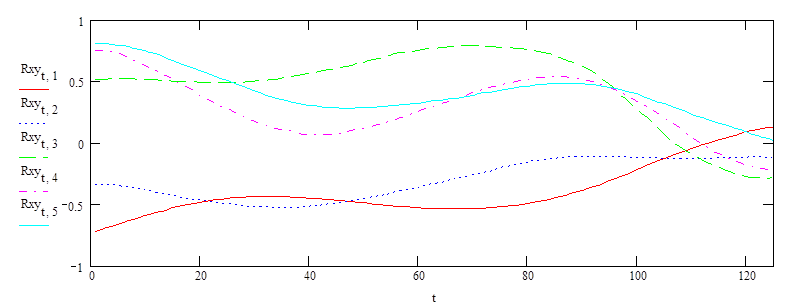
Рис. 4. Взаимно-корреляционные функции для второго выходного параметра

-  для третьей выходной переменной

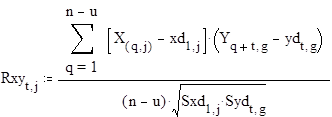
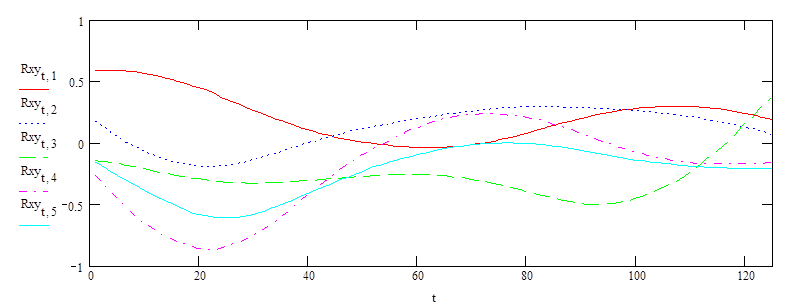
Рис. 5. Взаимно-корреляционные функции для третьего выходного параметра

-  для четвертой выходной переменной (в процессе расчета была ошибка, повтор для g=3 !)

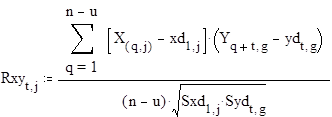
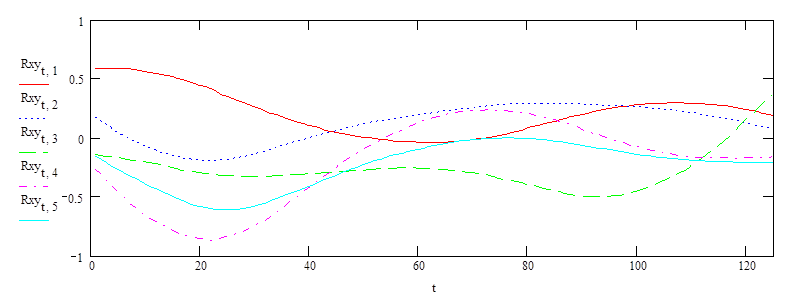
Рис. 6. Взаимно-корреляционные функции для четвертого выходного параметра

6. Определение времени наблюдения экспериментальных данных.

Самостоятельный выбор по графикам автокорреляционных и взаимно-корреляционных функций интервала съема данных (dt).

7.   Расчет средних значений и дисперсий переменных для выбранных данных

x - вектор средних значений матрицы X

 ,  

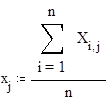y - вектор средних значений матрицы Y

,  

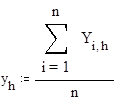Sx - вектор выборочных дисперсий матрицы X,

 ,  

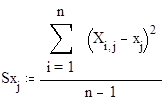Sy - вектор выборочных дисперсий матрицы Y

 ,

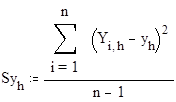7. Приведение данных к стандартному масштабу.

   

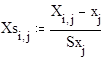
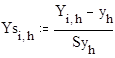
8. Расчет коэффициентов регресии для всех данных эксперимента.

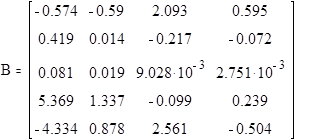
9. Проверка значимости уравнений регрессии по ковариационной матрице с помощью критерия Стьюдента и обнуление незначимых коэффициентов.

-  определение ковариационной матрицы

(по матрице t можно определить, какой из факторов /по строкам/ вносит минимальный вклад в результат эксперимента и, значит, его можно исключить)

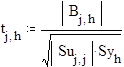
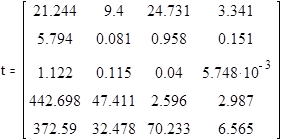
Номер этого фактора (задается вручную).

Определение новой матрицы  независимых переменных - X0, без одного исключенного фактора.

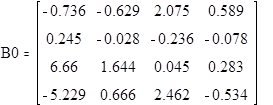
10. Проверка адекватности уравнений регрессии эксперименту с помощью критерия Фишера.

Soc1 ...  Soc4 -  остаточные дисперсии для 1 ... 4 уравнений регрессии соответственно.

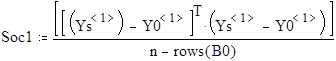
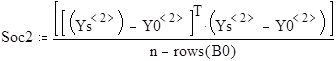
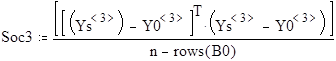
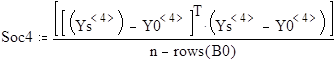
F1 ... F4 - значения коэффициентов Фишера для соответствующих уравнений регрессии .

Табличные значение коэффициента Фишера для данных g и l.

   

   

   

   

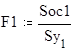
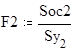
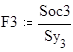
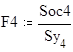
Самостоятельный вывод об адекватности уравнений регресии эксперименту

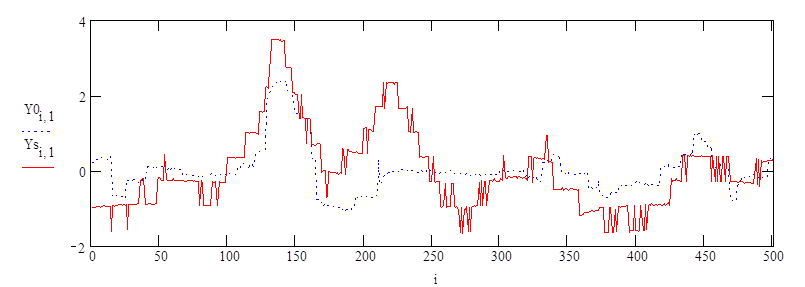
а)

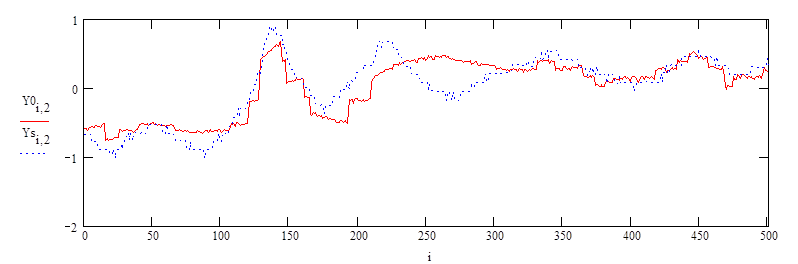
б)

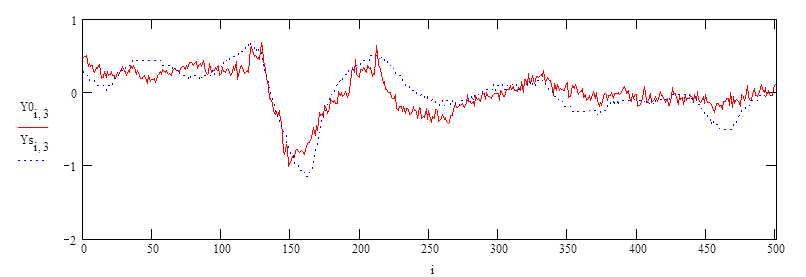
в)

Рис.7. Графики результатов эксперимента (пунктирные линии) и расчета (сплошные линии) по уравнениям регрессии для 1, 2 и 4 входных показателей

По результатам обработки записываются уравнения регрессии, делаются заключения об их адекватности эксперименту и о целесообразности стабилизации конкретных факторов.

Несовершенство данной обработки явно в подходе к выбору dt для всего массива данных. Целесообразно выделять обработку по каждому выходному показателю.