Министерство образования Российской Федерации

Группа: АА-06 Преподаватель:
Студент: Веселков А.П. Кондратьев В.А.
Отметка о защите: ……………………………
2003
Цель работы: Приобретение навыков организации, проведения и обработки результатов испытаний на основе положений пассивного эксперимента, построение автокорреляционной и взаимнокорреляционной функций входных переменных, получение уравнения регрессии.
Исходные данные.
1. Файл Lab_6.mdl, (структурная схема приведена в приложении 1).
расчет.
Расчеты всех параметров и величин, а также построение графиков зависимостей производятся с помощью M-файла, листинг которого приведен в приложении 1.
При обработке данных используются обозначения:
x1 – температура, создаваемая окружающей средой;
x2 – температура, создаваемая социальной средой;
у1 – температура, снимаемая с датчика;
у2 – почасовая стоимость;
1. Размер фрагмента данных выбираем n=720 , из того условия чтобы число переходов через среднее значение было 40-70. Во время моделирования получены следующие графики процессов (рис.1-3).
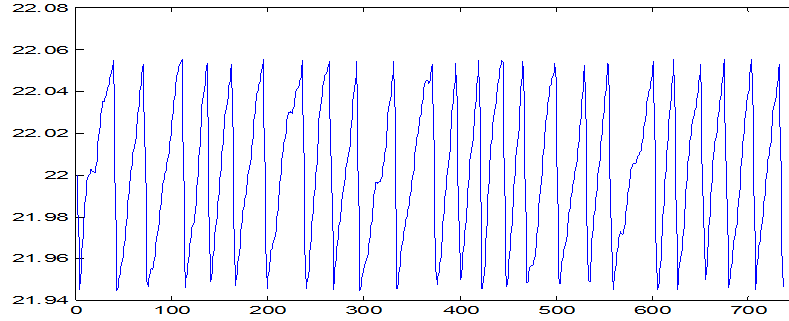
Рис. 1. График изменения выходной величины y1 (t°С в помещении).
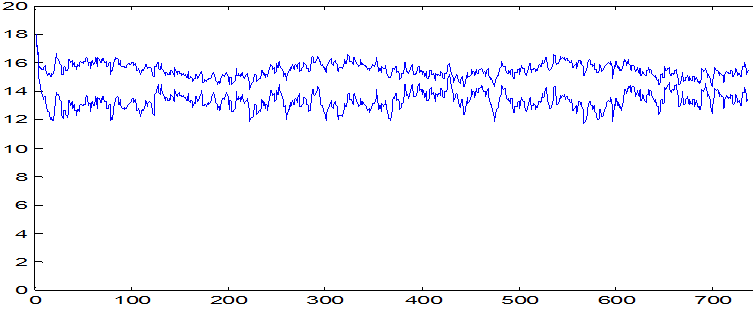
Рис. 2. График изменения входных величин y1.
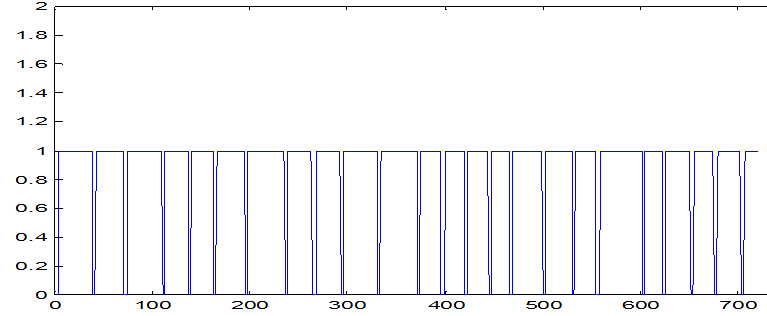
Рис.3. График изменения выходной величины y2.
Так как величина y2 не обладает инерционностью, то вычисление взаимнокорреляционных функций между y2 и входными величинами производить не будем.
2. Расчет средних значений и дисперсий для построения автокорреляционных и взаимнокорреляционных функций осуществляется по следующим формулам:
средние значения
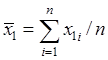 ,
, 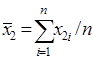 ,
, 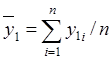 .
.
дисперсия
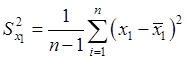 ,
,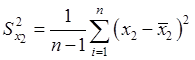 ,
,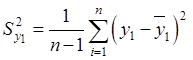 .
.
3. Расчет значений и построение автокорреляционных и взаимно корреляционных функций.
Выражение для нахождения взаимно корреляционной функции:
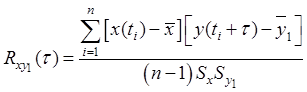 , где
, где ![]() – интервал регистрации данных;
– интервал регистрации данных;
n – число рассматриваемых наблюдений ![]() ;
;
![]() и
и ![]() –
рассеяние фактора и выходного показателя ОИ.
–
рассеяние фактора и выходного показателя ОИ.
Выражение для нахождения автокорреляционной функции:
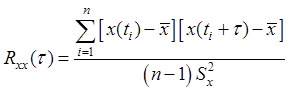 .
.
Графики взаимно корреляционных и автокорреляционных функций показаны на рис. 3-6.
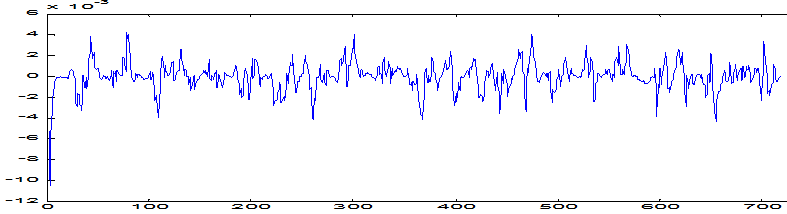
Рис. 3. График взаимной корреляции выходного параметра и влияния социальной среды
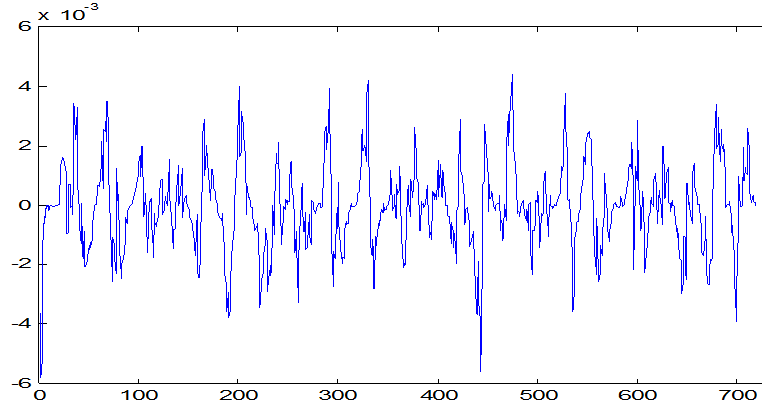
Рис. 4. График взаимной корреляции выходного параметра и влияния окружающей среды
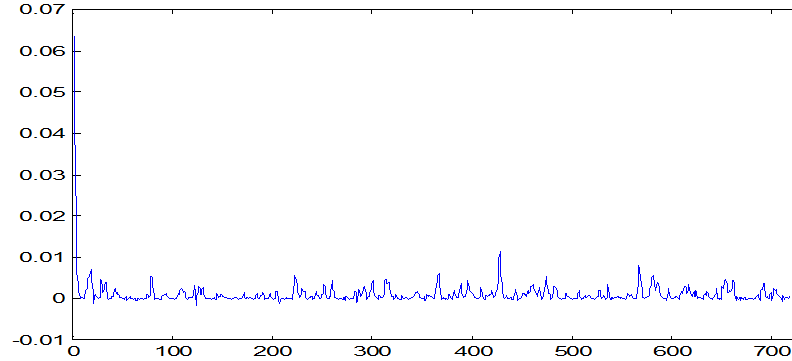
Рис. 5. График автокорреляционной функции влияния социальной среды
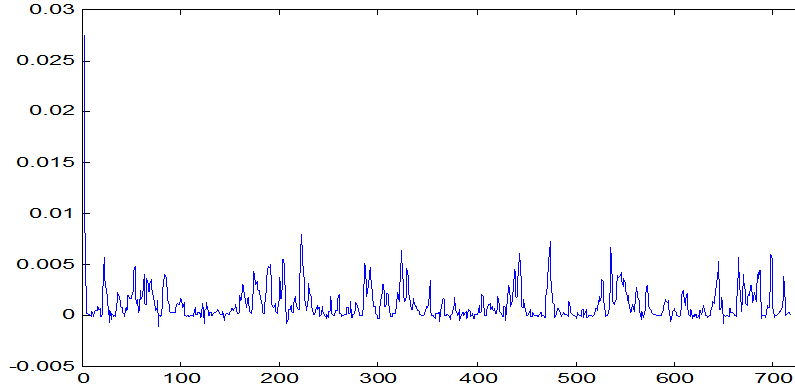
Рис. 6. График автокорреляционной функции влияния окружающей среды
Время корреляции для Rxx1(t) t0=1800c, а для Rxx2(t) t0=1080с.
Для непрерывных технологических процессов важен факт изменения тесноты корреляционной связи между входными и выходными величинами в зависимости от временного сдвига t между ними.
4. Переход к нормированному представлению данных осуществляется с помощью следующих выражений:
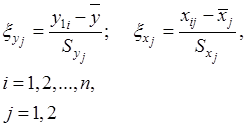
где ![]() – средние значения выходного показателя и
факторов;
– средние значения выходного показателя и
факторов;
![]() – рассеяния выборок.
– рассеяния выборок.
5. Расчет вектора коэффициентов уравнения регрессии осуществляется методом наименьших квадратов:
![]() , где
, где ![]() – соответственно
матрица сумм по размеру выборки нормированных значений факторов и столбец сумм
по размеру выборки нормированных значений выходной переменной.
– соответственно
матрица сумм по размеру выборки нормированных значений факторов и столбец сумм
по размеру выборки нормированных значений выходной переменной.
В
результате расчетов получена следующая матрица коэффициентов уравнения
регрессии 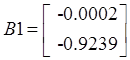 .
. 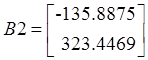
Коэффициент Стьюдента рассчитывается по формуле:
![]() .
.
Рассчитанные значения коэффициентов Стьюдента:
![]() ,
, ![]() .
.
Критерий Стьюдента ![]() . Первый коэффициент
регрессии являются статистически значимым, т.к. гипотеза
. Первый коэффициент
регрессии являются статистически значимым, т.к. гипотеза ![]() подтверждается, а второй
незначимый, однако исключать его нельзя из-за малого количества коэффициента
регрессии.
подтверждается, а второй
незначимый, однако исключать его нельзя из-за малого количества коэффициента
регрессии.
Таким образом, уравнения регрессии принимают вид:
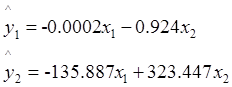
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.