Организация, проведение и обработка результатов испытаний на основе положений пассивного эксперимента, построение автокорреляционной и взаимнокорреляционной функций входных переменных, получение уравнения регрессии, страница 2

6.  Проверка адекватности полученного уравнения регрессии экспериментальным данным осуществляется проверкой гипотезы:

, где   – коэффициент Фишера ;

 – остаточная дисперсия ;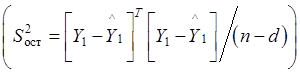

d – число коэффициентов регрессии (d  = 2);

 – столбец расчетных соотношений  ().

Табличное значение коэффициента Фишера: .  .

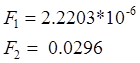Здесь коэффициент Фишера показывает, во сколько раз уменьшается дисперсия относительно полученного уравнения регрессии по сравнению с дисперсией относительно среднего значения результатов испытаний. Чем больше величина  по сравнению с критерием для доверительной вероятности p, числах степеней свободы  и , тем эффективнее уравнение регрессии.

, следовательно, гипотеза адекватности уравнения регрессии подтверждается.

Графики выходных переменных, построенных по исходным данным и выходных переменных, полученных с помощью расчёта по полученному уравнению регрессии, приведены на рис. 7 и  рис. 8

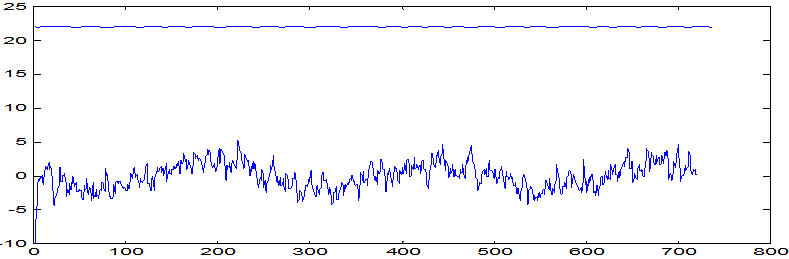
Рис. 7. Экспериментальная и расчетная кривые выходной переменной по температуре помещения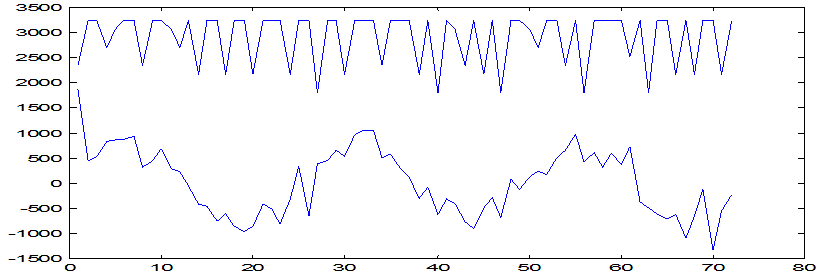

Рис. 8. Экспериментальная и расчетная кривые выходной переменной по стоимости

На рис. 7,8  видно, что реальная выходная переменная сильно отличается от выходной переменной, полученной с помощью расчёта по вычисленному уравнению регрессии, несмотря на то, что проверка гипотезы адекватности уравнений регрессии эксперименту дала положительный результат. Возможно, причиной тому служат параметры входных переменных и исследованный временной участок работы системы, на котором возможен большой разброс выходных параметров.

Уравнение регрессии точнее будет описывает реальный процесс в случае, когда выходные параметры процесса имеют меньший разброс. Также большей точности описания можно добиться изменением параметров входных величин с целью создания такого режима функционирования объекта, при котором колебания значений входных и выходных параметров будут меньше. То есть меньших отклонений между реальными выходными переменными (построенными по исходным данным) и выходными переменными, полученными с помощью расчёта по вычисленному уравнению регрессии можно добиться при изменении параметров входных величин.

Выводы:

1.  Взаимнокорреляционные функции факторов отличаются друг от друга.

2.  Получено уравнение регрессии вида:

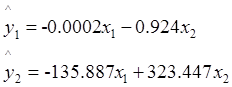
3.  Фактор x₁ наибольшим образом влияет на выходную переменную.

4.  Для регулирования исследуемого процесса целесообразно воздействовать на x₁.

Приложение 1.

Программа подсчета переходов температуры через среднее значение.

kon=720;

y=0;

kol=0;

for i=1:kon

y=y+rez(i,1);

end

y=y/kon;

for i=1:kon-1

if ((rez(i,1)>y)&(rez(i+1,1)<y))

kol=kol+1;

end  

if ((rez(i,1)<y)&(rez(i+1,1)>y))

kol=kol+1;

end

end

kol

Приложение 2.

Листинг программы

clc;

shag=360;

kon=720;

sum=0;

k=kon/(3600/shag);

s=zeros(k,1);

soc_k=zeros(k,1);

envir_k=zeros(k,1);

prise_new=zeros(kon,1);

for i=1:kon

prise_new(i,1)=prise(i+1,1)-prise(i,1);

if prise_new(i,1)>1 prise_new(i,1)=1;

end

end

%-------------------------------------------------for j=0:k-1

for i=1:9

s(j+1)=s(j+1)+(shag/2)*(prise_new(i+j*10,1)+prise_new(i+1+j*10,1));   %подсчёт стоимости методом трапеций

soc_k(j+1)=soc_k(j+1)+0.1*soc(i+j*10,1);                                                %создание нового массива значениё соц. среды

envir_k(j+1)=envir_k(j+1)+0.1*envir(i+j*10,1);                                       %создание нового массива окр.среды

end

sum=sum+s(j+1);                                                                                           %средняя цена за час

end

sum=sum/(kon/(3600/shag));

sum

%-----------------------------------Вычисление средних значений------------------------------------rez_sred=0;

soc_sred=0;

envir_sred=0;

prise_sred=0;

for i=1:kon

rez_sred=rez_sred+rez(i,1);

soc_sred=soc_sred+soc(i,1);

envir_sred=envir_sred+envir(i,1);

end

rez_sred=rez_sred/kon;

soc_sred=soc_sred/kon;

envir_sred=envir_sred/kon;

%---------------------------------------Вычисление дисперсий--------------------------------------------rez_disp=0;

soc_disp=0;

envir_disp=0;

s_disp=0;

4for i=1:kon

rez_disp=rez_disp+(1/(kon-1))*(rez(i,1)-rez_sred)^2;

soc_disp=soc_disp+(1/(kon-1))*(soc(i,1)-soc_sred)^2;

envir_disp=envir_disp+(1/(kon-1))*(envir(i,1)-envir_sred)^2;

end

for i=1:k

s_disp=s_disp+(1/(k-1))*(s(i)-sum)^2;

end

%-------------------------------------------------Вычисление взаимной корреляции---------------------------------------------------c1=zeros(kon-1,1);