Информатика и выч. техника \ Моделирование процессов и систем

Организация, проведение и обработка результатов испытаний на основе положений пассивного эксперимента, страница 2

F1=2.1*10-6;

F2=0.1469.

, следовательно, гипотеза адекватности уравнений регрессии подтверждается.

Графики выходных переменных, построенных по исходным данным и выходных переменных, полученных с помощью расчета по полученным уравнениям регрессии, приведены на рис. 8 и рис. 9.

  

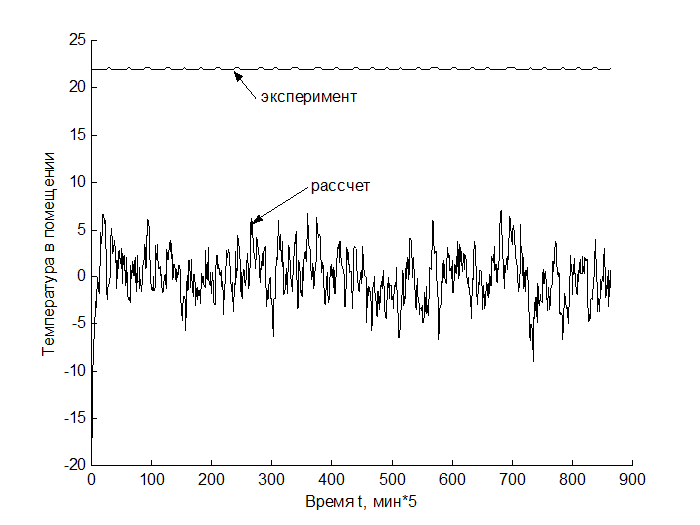
Рис. 8. Графики экспериментальной и расчетной температуры.

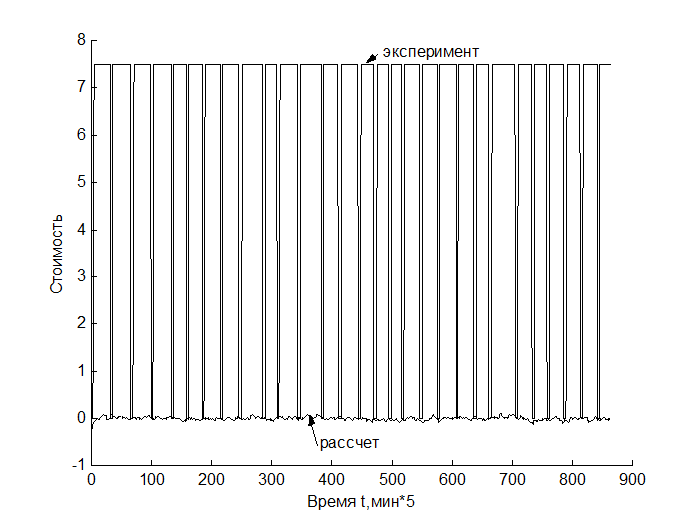
Рис. 9. Графики экспериментальной и расчетной стоимости.

Вывод:

В результате проделанной работы были получены следующие уравнения регрессии:

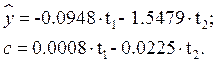
Коэффициенты этих уравнений по критерию Стьюдента оказались статистически незначимыми.

Данные уравнения регрессии адекватны экспериментальным данным. Они показывают, как изменяется положение среднего значения выхода с изменением входных величин. Из уравнения видно, что фактор t2 сильнее влияет на выходную характеристику, чем фактор t1. Поэтому для регулирования исследуемого процесса целесообразно воздействовать в большей степени на канал t2. 


Приложение 1

Текст программы обработки результатов пассивного эксперимента.

clc;

kn=864

ys=0;

for i=1:kn

ys=ys+out(i*300,1);

end

ys=ys/kn; %Среднее значение выходной переменной

n0=0;

for i=1:kn-1

if((out(i*300,1)>=ys)&(out((i+1)*300,1)<=ys))

n0=n0+1;

end

if((out(i*300,1)<=ys)&(out((i+1)*300,1)>=ys))

n0=n0+1;

end

end

i

n0  %Число пересечений среднего значений

for i=1:kn

y(i)=out(i*300,1);

end

tos=0;

for i=1:kn

tos=tos+to(i*300,1);

end

tos=tos/kn; %Среднее значение входной переменной 1

tos

for i=1:kn

tokr(i)=to(i*300,1); %Вектор выборочных значений фактора 1

end

tss=0;

for i=1:kn

tss=tss+ts(i*300,1);

end

tss=tss/kn; %Среднее значение входной переменной 2

tss

for i=1:kn

tsoc(i)=ts(i*300,1); %Вектор выборочных значений фактора 2

end

figure(1);

hold on;

plot(tokr(:));

plot(tsoc(:));

hold off;

figure(2);

plot(y(:));

ps=0;

for i=1:kn

ps=ps+Price(i*300,1);

end

ps=ps/kn; %Среднее значение выходной переменной 2

ps

for i=1:kn

pr(i)=Price(i*300,1); %Вектор выборочных значений выхода 2

end

figure(3);

plot(pr(:));

dsy=0;

dsto=0;

dsts=0;

dspr=0;

for i=1:kn % Подсчет дисперсий факторов и выходов

dsy=dsy+(1/(kn-1))*(y(i)-ys)^2;

dsto=dsto+(1/(kn-1))*(tokr(i)-tos)^2;

dsts=dsts+(1/(kn-1))*(tsoc(i)-tss)^2;

dspr=dspr+(1/(kn-1))*(pr(i)-ps)^2;  

end

for i=1:260 % Расчет автокорреляционных и взаимнокорреляционных функций

Ra_to(i)=0;

Ra_ts(i)=0;

Rv_to(i)=0;

Rv_ts(i)=0;

for j=1:kn-i

Rv_to(i)=Rv_to(i)+(1/((kn-1)*(dsto*dsy)^0.5))*((tokr(j)-tos)*(y(j+i)-ys));  

Rv_ts(i)=Rv_ts(i)+(1/((kn-1)*(dsts*dsy)^0.5))*((tsoc(j)-tss)*(y(j+i)-ys));  

Ra_to(i)=Ra_to(i)+(1/((kn-1)*dsto))*((tokr(j)-tos)*(tokr(j+i)-tos));

Ra_ts(i)=Ra_ts(i)+(1/((kn-1)*dsts))*((tsoc(j)-tss)*(tsoc(j+i)-tss));

end 

end

figure(4);

plot(Ra_to(:));

figure(5);

plot(Ra_ts(:));

figure(6);

plot(Rv_to(:));

figure(7);

plot(Rv_ts(:));

for i=1:kn % Нормирование потоков данных

ey(i,1)=(y(i)-ys)/dsy;

ey(i,2)=(pr(i)-ps)/dspr;

ex(i,1)=(tokr(i)-tos)/dsto;

ex(i,2)=(tsoc(i)-tss)/dsts;

end  

%Коэффициенты регрессии

b(:,1)=((ex(:,:)'*ex(:,:))^-1)*ex(:,:)'*ey(:,1);

b(:,2)=((ex(:,:)'*ex(:,:))^-1)*ex(:,:)'*ey(:,2)

c1=(ex(:,1)'*ex(:,1))^-1;

c2=(ex(:,2)'*ex(:,2))^-1;

for i=1:2

t1(i)=0;

t2(i)=0;

end  

%Коэффициенты Стьюдента

t1(1)=abs(b(1,1))/(dsto*sqrt(c1));

t1(2)=abs(b(2,1))/(dsts*sqrt(c1));

t2(1)=abs(b(1,2))/(dsto*sqrt(c2));

t2(2)=abs(b(2,2))/(dsts*sqrt(c2));

t1

t2

for i=1:2

if(t1(i)>1.96)

i

disp('Коэфициент b1 не значим');

end  

if(t2(i)>1.96)

i

disp('Коэфициент b2 не значим');

end

end

ym=ex(:,:)*b(:,:);%Расчетные значения выхода

figure(8);

hold on;

plot(ym(:,1));

plot(y);

hold off;

figure(9);

hold on;

plot(ym(:,2));

plot(pr);

hold off;

%Остаточная дисперсия

Sost1=((y(:)-ym(:,1))'*(y(:)-ym(:,1)))/(kn-2)

Sost2=((pr(:)-ym(:,2))'*(pr(:)-ym(:,2)))/(kn-2)

%Критерий Фишера

f1=dsy/Sost1

f2=dspr/Sost2

if(f1<1.2)

disp('Уравнение 1 адекватно');

end

if(f2<1.2)

disp('Уравнение 2 адекватно');

end

if(f1>=1.2)

disp('Уравнение 1 неадекватно');

end

if(f2>=1.2)

disp('Уравнение 2 неадекватно');

end


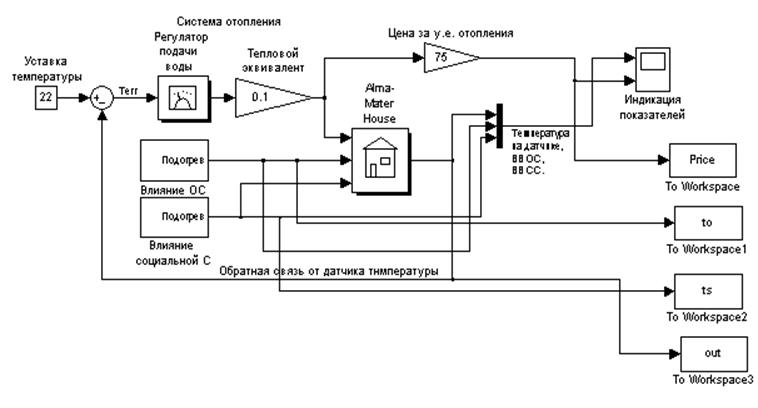
Приложение 2

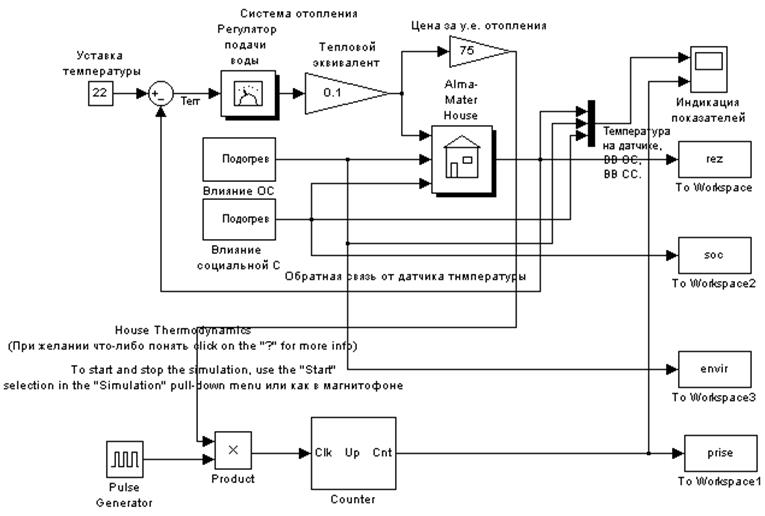
Исследуемая модель

Приложение 3

Модель объекта испытаний

Скачать файл