4. МОДЕЛИРОвание электромагнитного привода
4.1. Вводные положения
Синтез алгоритма управления электромагнитным приводом осложнен нелинейными свойствами компонентов, необходимостью учета ограничений его состояния и управления. Для его выполнения естественным представляется использование итерационных и эвристических приемов с анализом качества переходных процессов математическим моделированием свойств САУ. Широко применяемый в инженерной практике ПИД-регулятор не обеспечивает приемлемого качества переходных процессов электромагнитного привода. Предлагается поиск параметров цифрового регулятора для КЭМП проводить опосредованно через пересчет коэффициентов ХПЗС. Это предложение нуждается в пояснениях.
Множество регуляторов заданной структуры очень велико. Указать в нем подмножество, которое обеспечивает устойчивость САУ с конкретным ОУ, сложно. Множество желаемых (допустимых) эталонных моделей движения – существенно меньше. выбирать параметры из этого множества намного проще. Для пересчета коэффициентов ХПЗС нужны уравнения, связывающие коэффициенты модели ОУ, эталонной модели и искомого регулятора. Точное описание свойств ОУ не требуется, так как параметры регулятора определяются подбором. Для пересчета может быть использована линеаризованная модель ОУ. Метод линеаризации ОУ не имеет решающего значения, но необходимо, чтобы линеаризованная модель достаточно качественно воспроизводила свойства ОУ в области стационарного состояния САУ. Для проверки же работоспособности регулятора нужна более точная (адекватная) модель ОУ.
Если модель замкнутой САУ представить в полиномиальной форме (рис. 4.1), то для расчета параметров регулятора можно использовать решение полиномиального диофантова уравнения вида
A(Ч)D(Ч) + B(Ч)C(Ч) = L(Ч), (4.1)
где L(Ч) – желаемый характеристический полином замкнутой системы.
В этом уравнении предполагаются известными полиномы: A(Ч), B(Ч) и L(Ч). Полиномы D(Ч) и C(Ч) могут быть определены.
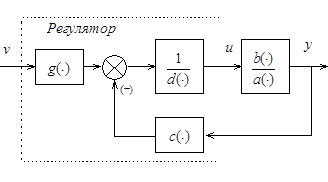
Рис. 4.1. Структурная схема САУ в полиномиальной форме
Связь коэффициентов регулятора, ОУ и САУ может быть задана посредством СЛАУ независимо от того, дискретная система или непрерывная. Поэтому в обозначениях полиномов опущен аргумент. Предпочтительной формой представления непрерывно-дискретных систем являются конечные разности. Соответствие задается формулой [19]:
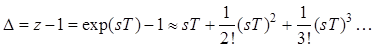 .
.
Если обозначить через cT, dT, L T вектор-столбцы, составленные из коэффициентов соответствующих полиномов, то из (4.1) можно получить:
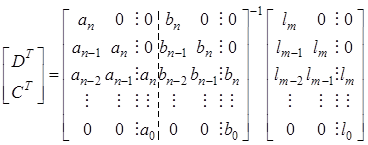 .
.
Отсюда следует, что, задавшись коэффициентами или корнями ХПЗС, можно рассчитать неизвестные коэффициенты регулятора. При выборе структур полиномов необходимо учитывать условие физической реализуемости регулятора, согласно которому степень полинома D(Ч) не может быть меньше степени полинома C(Ч). Кроме того, обращение матрицы также налагает ограничение на применение этого метода: матрица должна быть невырожденной.
Анализ СЛАУ, связывающей коэффициенты ОУ, регулятора и ХПЗС, показывает, что по условию существования решения минимальный порядок регулятора составляет n-1 (n − порядок ОУ). При этом все коэффициенты регулятора связаны СЛАУ и ни один из них не может быть задан произвольно. Чтобы получить возможность задавать статическую точность замкнутой САУ, необходимо увеличить число уравнений (повысить порядок регулятора). Тогда появятся свободные коэффициенты, задавая которые, можно менять статический коэффициент или повышать порядок астатизма. Общее количество корней ХПЗС минимум 2n-1, максимум не ограничен, но усложняет регулятор. Для статического ОУ лучше задать 2n корней, тогда регулятор будет астатическим. Для астатического ОУ приемлемо 2n-1.
Собственно пересчет может быть выполнен следующей подпрограммой-функцией:

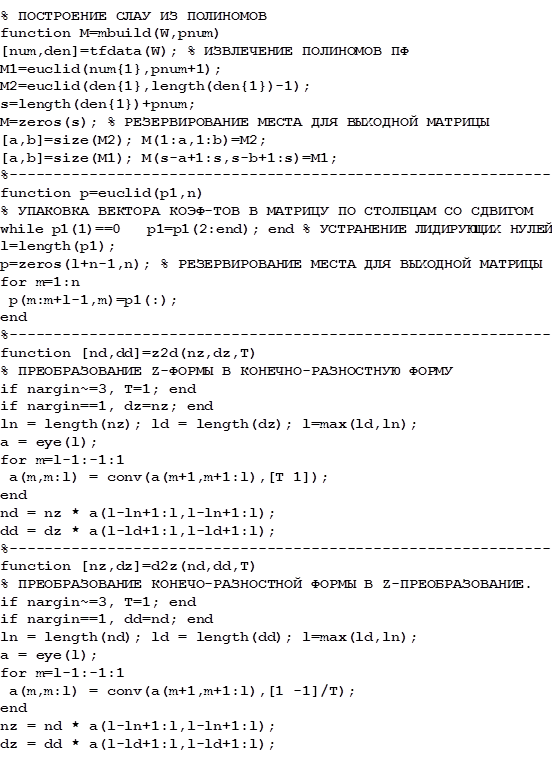
Для решения задачи необходимо иметь линеаризованную модель ОУ и задать желаемый ХПЗС или его корни.
Представленная во втором разделе функция linmod реализует классический подход линеаризации «в малом» в окрестностях рабочей точки. Однако применительно к КЭМП возможностей этой функции недостаточно. Это обусловлено главным образом свойствами ЭМД, составленного из двух ЭМС, а также параметрическим заданием свойств каждой из них семейством интерполированных характеристик L(i, δ), K(i, δ) и Fэм(i, δ). Приближенная модель КЭМП может быть воспроизведена структурно со значениями параметров, примерно соответствующих стационарному состоянию привода.
Подход к расчету регулятора на основе заданного расположения полюсов замкнутой системы известен относительно давно [18]. Несколько реализаций имеется и в среде MATLAB (подпрограммы-функции placeиacker).
Можно сформулировать общие рекомендации по размещению корней ХПЗС. Основное время на переходный процесс определяют корни около точки 1 (см. рис. 2.6). Вместо пары вещественных корней лучше задать комплексно-сопряженные. Такое решение уменьшит время переходного процесса, но следует при этом учитывать, что чрезмерное увеличение мнимой части приведет к повышению колебательности системы. Желательно корни разбить на 2 группы и разнести их. Это увеличит запас устойчивости. Наивысшее быстродействие может быть обеспечено при размещении корней в центре круга. Это обусловлено тем, что составляющие движения, соответствующие корню в центре круга, затухают за один такт.
Алгоритм итерационной процедуры поиска коэффициентов регулятора состоит из трех последовательных шагов: во-первых, задаются корни желаемого ХПЗС; во-вторых, с использованием линеаризованной модели ОУ рассчитываются коэффициенты регулятора; в-третьих, с использованием точной модели ОУ рассчитывается и анализируется переходный процесс. Реализация этого алгоритма с ориентацией на параметры макетного образца КЭМП представлена программой:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.