Разработка и синтез регулятора для двухканальной системы, состоящей из трех масс, полиномиальным методом синтеза

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Автоматики

Расчетно-графическая работа

по курсу: «Многоканальные системы»

Факультет:   АВТ

Группа:         ААМ-10

Студент:                                                                                  Преподаватель:

Солдаткин А. А.                                               Воевода А.А.

Новосибирск 2010

№	Дата	Содержание	Примечание

Цель работы: разработать и синтезировать регулятор для двухканальной системы, состоящей из трех масс полиномиальным методом синтеза.

Постановка задачи

В качестве объекта управления взята трехмассовая система (рис. 1), в которой два управляющих сигнала, силы u₁ и u₃, приложены к первой и третьей массам m₁и m₃, подвешенным последовательно на трех пружинах жесткостью k₁, k₂ и k₃, а регулируемые величины – положения двух верхних грузиков.

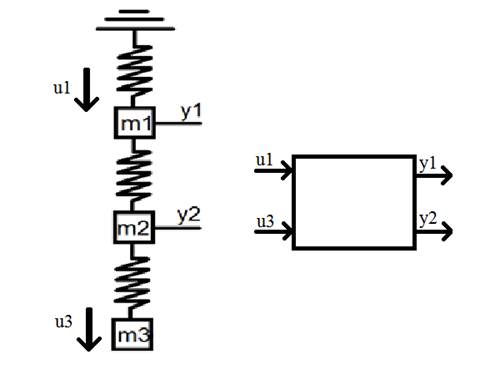
Рис. 1. Схематичное изображение физического объекта управления.

Зададим значения параметров объекта:

m₁= 4                     k₁ = 2

m₂= 2                     k₂ = 2

m₃= 2                     k₃= 2

Модель объекта

В качестве объекта управления возьмем систему из трех масс , последовательно соединенных пружинами жесткостью . Массы, а также их координаты  пронумерованы сверху вниз. Предполагается два управляющих сигнала – силы u₁ и u₃, приложенные к массам m₁ и m₃. Демпфирование равно нулю. Управляемыми величинами будем считать координаты грузов  и , отсчитываемые от состояния равновесия. [1]

Перейдем к изображениям:

Сгруппируем переменные:

Умножив второе уравнение на множитель , исключим переменную  из системы:

Запишем матричную передаточную функцию в полиномиальном виде:

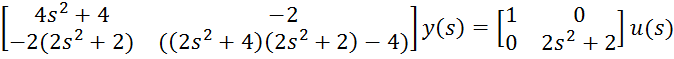, или, в матричных обозначениях:

, что соответствует левому полиномиальному разложению. Здесь

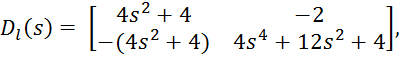
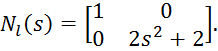
Отнормируем эти матрицы, разделив их на 4:

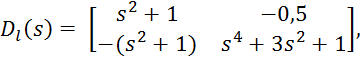
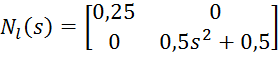
Найдем detD_l(s):

, что соответствует трем парам комплексно сопряженных полюсов:

Вырождение матрицы N_l(s) происходит при 0,125s²+0,125, что соответствует нулям ±j. Таким образом, имеются совпадающие нули и полюсы у объекта, принадлежащие замкнутой правой полуплоскости, следовательно, достаточное условие разрешимости задачи автономизации не выполнено.

Нами найдено левое разложение матричной передаточной функции:

Найдем правое полиномиальное разложение объекта:

Для этого необходимо рассмотреть матрицу , которую элементарными операциями над столбцами следует привести к нижнетреугольному виду

, что соответствует умножению исходной матрицы на полиномиальные матрицы с определителем, равным вещественному числу (унимодальные матрицы), справа. Допустим, нам удобнее выполнять операции над строчками. Исходную матрицу транспонируем , тогда задача приведения к нижнетреугольному виду заменится на задачу приведения  к верхнетреугольному виду, а операция умножения справа на унимодальные матрицы заменится на задачу умножения слева на унимодальные матрицы.

Приведем матрицу  к верхнетреугольному виду:

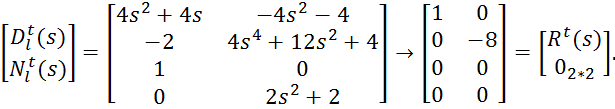
В ходе преобразования использовались следующие матрицы:

;	;
;	;
;	.

Найдем результирующее преобразование :

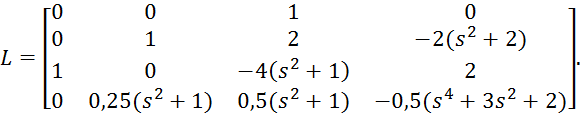
Для проверки умножим  слева на (-функция от !) и получим тот же результат , или

.

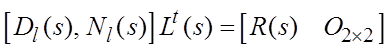Здесь

.

.

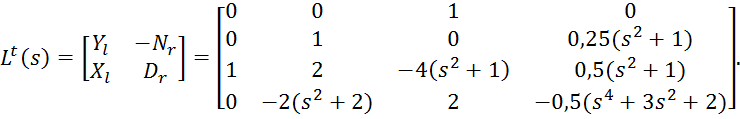
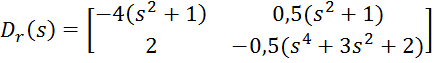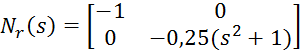Получено правое взаимно простое разложение матричной передаточной функции объекта.

Синтез регулятора

Отнормируем матричную передаточную функцию объекта, представленную в виде правого разложения – умножим «числитель»  и «знаменатель»  на «–2». В результате коэффициент при старшей степени s⁴ окажется равным единице:

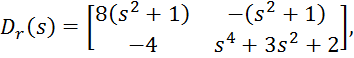
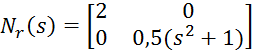
Запишем матрицы  и  в полиномиальном виде

,.

Здесь

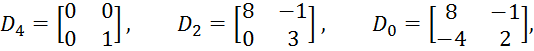
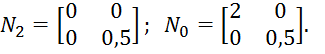
Опишем систему уравнениями

 , где – выход объекта, – выход регулятора, – задание.

Найдем передаточную функцию системы:

.

Задав регулятор в виде левого полиномиального разложения  , получим

.

Выберем структуру «числителя» и «знаменателя», т. е. выберем порядки, например равными трем и трем: