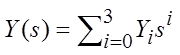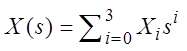Разработка и синтез регулятора для двухканальной системы, состоящей из трех масс, полиномиальным методом синтеза, страница 2

, .

Таким образом, при известном правом представлении объекта в предположении, что ищем регулятор в виде левого разложения, задача синтеза сводится к решению диофантова уравнения:

.

Здесь – характеристическая матрица системы размером 2 на 2. Приравняв коэффициенты при одинаковых степенях s, получим систему уравнений, которая в матричном виде запишется так: . Далее следует решать диофантово уравнение, выбирая каким-либо образом степени матриц ,  .

Запишем диофантово уравнение в матричном виде:

.

.

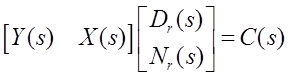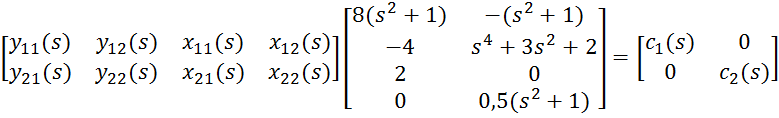Выберем степени полиномов регулятора ∂(C_i(s)) = 5. Тогда очевидно, что

,

.

.

Можем выписать “структуру” матриц  и :

,                   

.

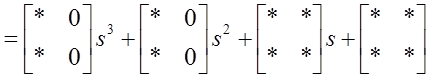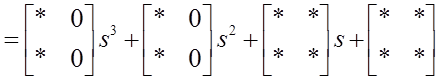где звездочками помечены элементы, подлежащие определению.

Тогда:

.

Приравняв коэффициенты при s с одинаковыми степенями в левой и правой части получим систему линейных уравнений, которую можно записать в матричном виде

.                                           

Здесь:

, ,

.             

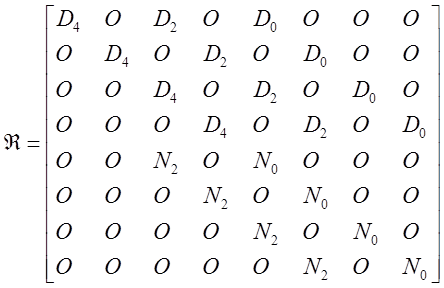Так как вторые столбики матриц , , ,  - нулевые нулевыми же являются значения столбиков 2, 4, 10, 12 матрицы :

   .

При умножении  на  строки 2, 4, 10, 12 матрицы  не важны для нас и их можно выбросить вместе со столбцами 2, 4, 10, 12 матрицы . После этого столбцы 1, 2, 3, 4 матрицы  оказываются нулевыми. Следовательно, столбцы 1, 2, 3, 4 матрицы  должны оказаться нулевыми – это ограничение на выбор матрицы . В итоге мы обязаны выбросить из матриц  и  столбцы 1, 2, 3, 4.

Матрицу  после выбрасывания столбцов 2, 4, 10, 12 обозначим через :

 

,

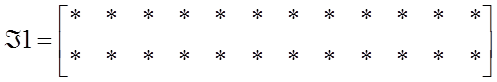Матрицу  после выбрасывания строк 2, 4, 10, 12 и столбцов 1, 2, 3, 4 обозначили через :

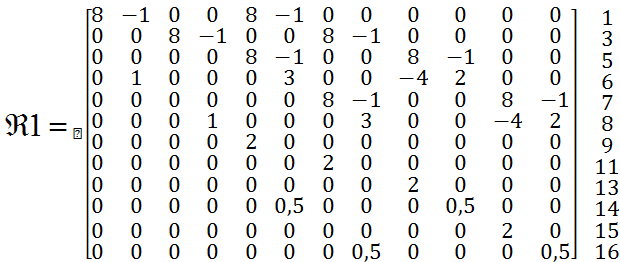
Матрицу  после выбрасывания столбцов 1, 2, 3, 4 обозначим через :

 

.

Получили систему уравнений . Проверим матрицу  на вырожденность - . Нужно убрать две линейно зависимые строки. По очереди убирая по одной строке из матрицы , выясняем, что  при удалении строк 5, 7, 9, 11, 13, 14, 15, 16 (в исходной нумерации) ранг не понижается. Следовательно, строки нужно убирать из этого набора. Теперь будем убирать по две строки в матрице  из набора 5, 7, 9, 11, 13, 14, 15, 16. При удалении строк 7 и 14 (нумерация строк сохранена из матрицы ) ранг остается равным 10. Следовательно, строки 7 и 14 линейно зависят от остальных строк. В уравнении  в матрице  им соответствуют столбцы 7 и 14, т.е. первый столбик  (обозначим ) и второй столбик  (обозначим ). Левую часть  можем представить в виде двух частей:

.

Здесь:

,

,

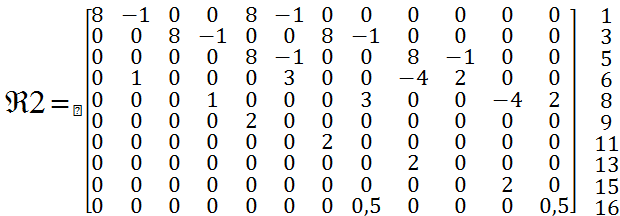
Ранг матрицы  равен 10, а столбцов – 12. Найдем линейно зависимые столбцы. Это столбцы 6 и 8 в исходной нумерации. Из представления левой части уравнения в виде двух слагаемых следует, что 6 и 8 столбики в  произвольно задавать нельзя. Тогда преобразуем само уравнение:

.

Из выше сказанного следует, что из  и  исключаем столбики 6 и 8, в результате чего получаем уравнение

, где . Матрицы  и  получены из  и  вычеркиванием 6 и 8 столбцов:

=

+

   

.

 

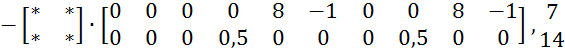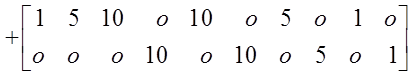Полином задали равным . Полином  можно задать только частично:

*s⁵ + *s⁴ + 10s³ + 10s² + 5s + 1.

Задать коэффициенты при  и  произвольно мы не можем. Нам необходимо задать матрицу  - часть параметров регулятора. Выберем  равной единичной матрице. Тогда

1             3          5          6            8          9        11      13        15        16

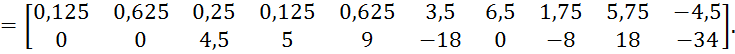
Чтобы восстановить , следует вспомнить, что столбики 2, 4, 10, 12 – нулевые, а 7 и 14 – составляют матрицу :

                 

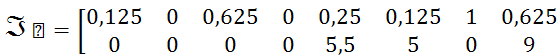
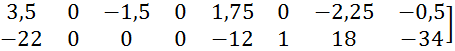
Вспомнив структуру , , : ,

, , можем выписать “числитель” и “знаменатель” регулятора:

,

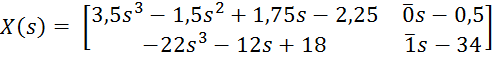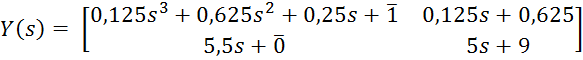
Помеченные числа – это элементы матрицы , заданной произвольно – в нашем случае  приравняли к единичной матрице. Найденное решение  зависит от выбора . Вычислим C(s):

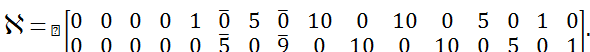
Помечены числа, которые мы не можем задавать произвольно, т.к. их значения зависят от выбора  и внутренних зависимостей. По матрице  несложно восстановить характеристическую матрицу :

.

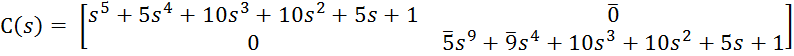Выделенные коэффициенты произвольно задавать не можем. Таким образом, по второму каналу получили полином

, характеристические числа которого:

.

Как ни странно, но перекрестных связей в системе нет.

Список использованной литературы

[1] Воевода А.А, Ижицкая Е.А О разрешимости задачи автономизации многоканальной системы ч.1 // Сб. науч. тр. НГТУ. – 2010. – № 2(60). – С. 9–15.

[2] Воевода А.А, Шоба Е.В. О разрешимости задачи автономизации многоканальной системы ч.2 // Сб. науч. тр. НГТУ. – 2010. – № 3(61). – С. 25–34.