Структурная теорема. Реализация матричной передаточной функции T(s). Представление дифференциальными операторами. Переход от дифференциальных операторов к пространству состояний. Управляемость и наблюдаемость

1. Структурная теорема:

Для пространственного представления A,B,C,D управляемой системы с В полного ранга передаточная функция T(s)=C(sI-A)^-1 B+D может быть представлена так:

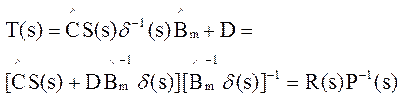
Получили объект в виде правого полиномиального разложения.

Свойства матриц R(s) и P(s):

1.P(s) –полиномиально-столбцово-правильная;

2.степень каждого столбца R_j(s) ≤ степени соответствующего столбца P_j(s).

Из управляемости матрицы следует существование невырожденного преобразования Q к системе в управляемой сопровождающей форме:

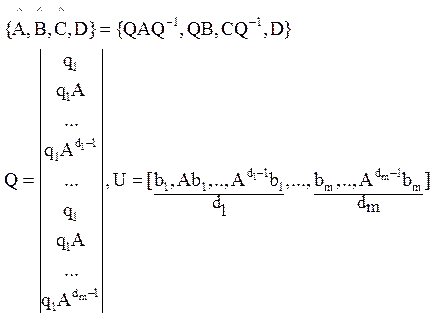
Q-управляемая сопровождающая форма, q_i - -ая строка из U^-1, U получена из матрицы управляемости перестановкой столбцов, d_i–индексы управляемости, .

Из выделили  и из выделили

размерами m*n (m упорядоченных строк с номерами из и ).-  верхне-треугольная с единичной диагональю.

 

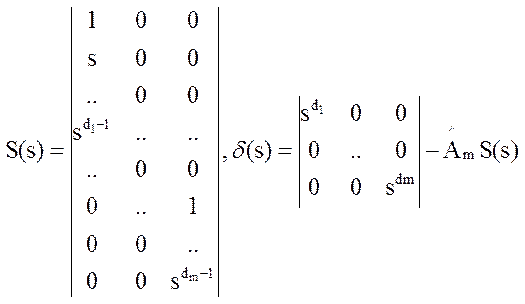
Примечание: Можно использовать наблюдаемою сопровождающую форму и получить аналогичную теорему.

2.Реализация матричной передаточной функции T(s):

Это любое представление в пространстве состояний {A,B,C,D}, чья матричная передаточная функция есть T(s).

Реализации могут быть управляемые, наблюдаемые, минимальные, канонические, неканонические.

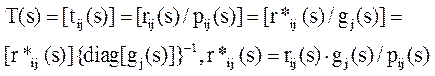Получив правое полиномиальное разложение для матричной ПФ можем использовать структурную теорему для получения описания в пространстве состояний.

=.

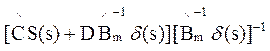Так как -столбцовоправильная

(из свойств струк. теоремы).

(Г_с-матрица коэффициентов при степенях столбцов), то есть .

Введем обозначения d_i ∆ , тогда

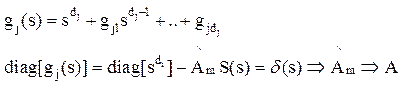Из правильности T(s) следует

, таким образом

.

.

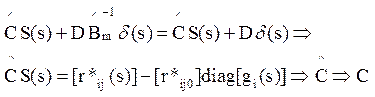Справедливы следующие теоремы:

1. n-мерная реализация {A,B,C,D} матрицы T(s) минимальная тогда и только тогда, когда она управляема и наблюдаема, т.е. когда размерности пространств управляемости и наблюдаемости равны n.

2. Если {A,B,C,D}-минимальная реализация для T(s), тогда - минимальная реализация в том и только том случае, если эти две реализации эквивалентны, т.е. существует такое невырожденное Q, при котором .

Примечание: Матрица А минимально реализована, если имеет минимальную размерность.

3.Представление дифференциальными операторами:

Часто используется описание в операторном виде

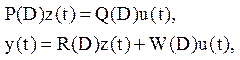(1)

где D=d/dt – оператор дифференцирования; P(D)-невырожденная матрица (q*q);Q(D)- матрица (q*m) и R(D), W(D)-матрицы (p*q) и (p*m). Возникает естественный вопрос о переходе к представлению в нормальной форме  (2) и наоборот. Матричная передаточная функция системы, вычисленная по (1) и (2) представляет собой

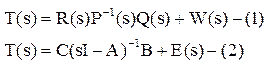
Вектор x(t) можно восстановить по z(t) и u(t) при помощи некоторых матриц в случае полной наблюдаемости системы

При переходе от одного состояния в другое необходимо обеспечить, чтоб при одном и том же входном сигнале на входе можно было выбрать такие начальные условия, при которых бы выходы этих систем совпадали.

Справедлива теорема:

Любой дифференциальный оператор системы в форме (1) имеет эквивалентное представление в пространстве состояний (2).

Примечание:

Процедура перехода в следующем билете.

4.Переход от дифференциальных операторов к пространству состояний

Любой дифференциальный оператор системы в операторной форме

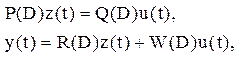имеет эквивалентное представление в пространстве состояний. Процедура перехода состоит в следующем:

Шаг1.Если P(D) строчноправильная-переход на шаг2, в противном случае P(D) умножается слева на унимодальную матрицу и приводится к строчноправильной.

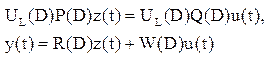 (1)

Шаг2.Пусть z₀(t)=Г_rz(t), где Г_r –(q*q) невырож. матрица из коэфф. при высших степенях D строк U_L(D)P(D). Если Г_r=I, то перейти к шагу3. В противном случае подставим Г_r^-1z₀(t)=z(t) в (1) (не нарушает эквивалентности):

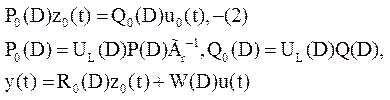
В полин. мат. P₀(s) по диаг.стоят эл-ты с высшими степ. по D в каждой стр..

Шаг3.Из (2) z₀(t)=P₀^-1(s)Q₀(s)u(s).Если P₀^-1(s)*

Q₀(s)-строго правильная (), переходим к шагу4. Иначе выделяем строго правильную часть  из P₀^-1(s)Q₀(s):

, где H₀(s)-полиномиальная матрица.

 Подставим z₀(t) в (2) и с учетом :

.Если ввести ∆ R₀(D)H₀(D)+W(D): .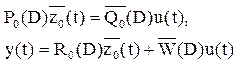

Шаг4. Из строгоправильной передаточной матрицы можем получить наблюдаемую реализацию {A₀,B₀,C₀}. Запишем P₀(s)  в виде:

 

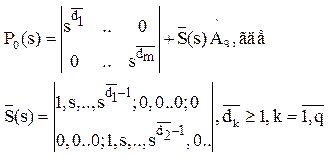
Получим { A₀,B₀,C₀}:

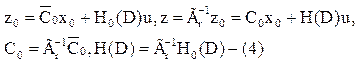
таким образом, получили

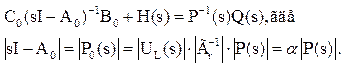
Шаг5.Подставим (4) в (1)

, используя зависимость (3) получим

.

В результате получено описание системы в пространстве состояний { A,B,C, E(D)}.

5. Управляемость и наблюдаемость

Рассмотрим описание системы в операторном виде и в пространстве сост.

   

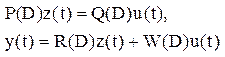
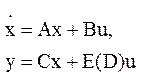
Теорема: Рассм. систему в операторном виде. Любое эквивалентное представление в форме пространства состояний:

а) полностью управляемо тогда и только тогда, когда любой наибольший общий левый делитель G_L(D) матриц P(D) и Q(D)-унимодальная матрица.

б) полностью наблюдаема тогда и только тогда, когда любой наибольший общий правый делитель G_R(D) для R(D) и P(D) – унимодальная матрица.

в) минимально тогда и только тогда, когда (а) и (б) имеют место.

Следствие. Любая система в форме пространства состояний.

а) полностью управляема, если и только если любой наибольший общий левый делитель матриц (sI-A) и B-унимодальная матрица;

б)полностью наблюдаема, если и только если любой наибольший общий правый делитель для (sI-A) и C-унимодальная матрица.