Структурная теорема. Реализация матричной передаточной функции T(s). Представление дифференциальными операторами. Переход от дифференциальных операторов к пространству состояний. Управляемость и наблюдаемость, страница 2

в) минимальна тогда и только тогда, когда (а) (б) имеют место.

Определение. Рассмотрим операторное представление. {P,Q,R,W} называются:

а) наблюдаемым дифференциальным операторным представлением, если и только если любой наибольший общий правый делитель для P(D) и R(D)-унимодальная матрица;

б) управляемым дифференциальным операторным представлением, если и только если любой наибольший общий левый делитель для P(D) и Q(D)-унимодальная матрица.

в) минимальным дифференциальным операторным представление , если и только если (а) (б) имеют место.

6. Приведение скалярной передаточной функции к взаимно простому виду

Пусть H(s)-некоторая перед. функция, которую запишем в виде

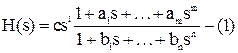
где  и c - комплексные константы с , m и n - неотрицательные целые, 1-некоторое целое. Задача состоит в определении коэффициентов c₁..c_p,d₁..d_q, таких, что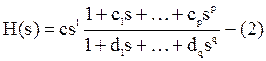    

где  и  взаимно простые. Алгоритм включает в себя пять шагов.

Шаг1. Предположим, что . Тогда мы запишем так называемую би-теплицеву матрицу  размерами

(m+n)*(m+n+1) следующим образом:

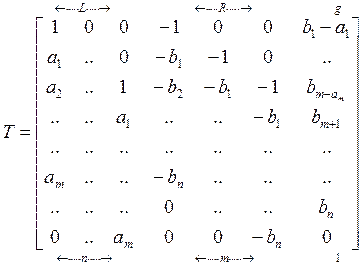Если , достаточно перейти к рассмотрению обратной передаточной функции, т.е. поменять местами  и . Таким образом, мы всегда сформируем матрицу T такую, что ширина блока L будет меньше ширины блока R.

Шаг2. Используем строчные операции над T с целью преобразования ее к виду T₀ со следующей формой:

  

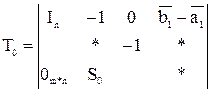
где I_n-единичная матрица (n*n), 0_m*n-нулевая матрица (m*n), S₀-блок (m*m). Так как L теплицева матрица, то все её диагональные элементы равны 1.

Шаг 3. Определим ранг S₀. Если S₀ имеет полный ранг, то вычисления окончены. Передаточная функция H(s), заданная (1), уже несократима. Если S₀ неполного ранга, тогда удаляем последний столбец из R₀ и две последние строки из T₀

Шаг 4. Проверим ранг S₁. Если S₁ имеет полный ранг, тогда продолжим строчные операции над T₁ с целью получения

Если S₁- неполного ранга, тогда удаляем последний столбец L^-1, последний столбец R¹ и две последние строки T₁, получая T₂=[L²|R²|g²].

Шаг 5. Повторим процедуру шага 4 k-раз, до тех пор, пока не получим матрицу T_k¹ размерами

 

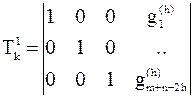
и результат:

7. Преобразование матрицы к строчно приведенному виду.

Каждая несингулярная (квадратная) полин. матрица D(s) может быть преобразована к строчно приведенному виду исключительно столбцовыми операциями. Другими словами, существуют унимодальные матрицы U(s) и V(s) такие, что U(s)D(s) и V(s)D(s) строчно приведенные. Процедура преобразования D(s) к эрмитовой форме (верхнетреуг. матрица) посред. элемент. столбц. операций может быть использована для вычисления матрицыV(s). ПустьD(s) – полином. матрица размерами (p*p)со строчными степенями v_i, обозн-ми как Обозначим

Запишем

                                                  

где  I – (p*p) единичная матрица. Мы отметим, что большинство строк I_i нулевые. Матрица D(s) строчно приведенная, если и только если D_o несингулярная. Cформируем строчную матрицу

и поставим в соответствие каждой строке В ее строчную степень v_i.

Шаг1. Переставим строки  В и соотв. им v_i так, чтобы  .

Шаг2. Найдем ненулевой элемент, называемый ведущим элементом, в первой строке D_o и затем исключаем, используя элементарные строчные операции над В, все элементы ниже его. Затем находим ненулевой ведущий элемент во второй строке D_o и исключаем все элементы ниже его. Повторяем эту процедуру до достижения последней строки D_o. Если D_o появится нулевая строка, идти на шаг 3. Если нулевая строка не появилась в D_o, идти на шаг 4.

Шаг3. Если нулевая строка  появилась в D_o, аналогичная строка в I_o, будет также нулевой. Мы смещаем эту строку из В налево на 2pпозиций и уменьшаем соответствующее  v_i  на 1 и идем на шаг 1.

Шаг 4. По полученным D_i, I_i и v_i формируем

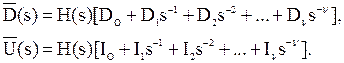
После этого имеем , причем  строчно приведенная.

Примечание. Очевидно, что алгоритм, приведенный в этом разделе, может быть модифицирован таким образом, чтобы находить унимодальную матрицу V(s) такую, что D(s)V(s) , будет столбцово приведенной. Заданное разложение D^-1(s)N(s), если N(s) дано в соответствии с (12) и В(s) в соответствии с (14), может быть представлено так:

Таким образом, алгоритм приводится к

где  строчно приведенная матрица.

8. Синтез компенсатора типа «вход-выход обратной связи»

Идея: разложить знаменатель замкнутой системы на два множителя: знаменатель и сокращаемую часть.

Пусть объект строго правильный , где D(s) и N(s) – взаимно простые справа и D(s) – столбцово приведенная со столбцовыми степенями . Тогда передаточная функция компенсатора может выглядеть так:

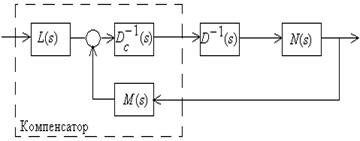
1) Выбирается желаемый знаменатель замкнутой системы F(s) так, чтобы столбцовые степени F(s) были равны столбцовым степеням D(s).

2) Выбирается гурвицева матрица D_c(s), которая должна быть строчно приведенная со строчными степенями ν-1, где ν-индекс наблюдаемости объекта.

3) Находятся L(s) и M(s) из уравнения .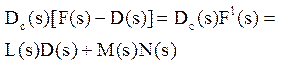

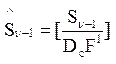Преобразуем . Воспользовавшись строчным поисковым алгоритмом, получаем , где и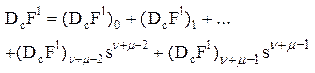

Вычисление L(s) и M(s) – это основная процедура синтеза. Для их нахождения существуют и другие методы, которые позволяют уменьшить порядок компенсатора для заданного знаменателя системы.