13. АЛГОРИТМ ДЕЛЕНИЯ ПОЛИНОМИАЛЬНЫХ МАТРИЦ
Рассмотрим пару полиномиальных матриц R(s) и P(s), где R(s)
(p * m) и P(s) (m * m)
несингулярная. Деление R(s) на P(s) справа
определяет единственную пару полиномиальных матриц, называемых остатком
(remainder) ![]() и частным (quotient)
и частным (quotient)
![]() :
:
![]() (1)
(1)
![]() (2)
(2)
с ![]() строго правильной рациональной матрицей.
строго правильной рациональной матрицей.
Основная
цель этого раздела – представить алгоритм определения ![]() и
и
![]() посредством выполнения операции умножения
над вещественными матрицами. При этом желательно избежать операции обращения
как в явном, так и в неявном виде.
посредством выполнения операции умножения
над вещественными матрицами. При этом желательно избежать операции обращения
как в явном, так и в неявном виде.
Пусть
![]() обозначает степень i-го
столбца P(s) для
обозначает степень i-го
столбца P(s) для ![]() :
:
![]() (3)
(3)
Далее мы полагаем, что P(s) столбцово правильная и что
![]() (4)
(4)
При этих двух предположениях может быть найдено управляемое и наблюдаемое представление в пространстве состояний для преобразования Лапласа дифференциального оператора системы.
P(s)z(s)=u(s) (5)
или, эквивалентно, минимальная реализация в пространстве состояний для матричной передаточной функции P-1(s), где
![]() (6)
(6)
может быть определена
посредством использования «структурной теоремы», что будет далее
проиллюстрировано примером. Более точно, можно найти вещественные матрицы А
и В в управляемой сопровождающей форме для многоканальных систем
(multiinput controllable companion form) и соответствующую «выходную» матрицу СI, которые определяют систему в пространстве состояний порядка ![]() , а именно:
, а именно:
![]() (7)
(7)
Здесь (7) эквивалентно (5) и реализует (6) в смысле, что если
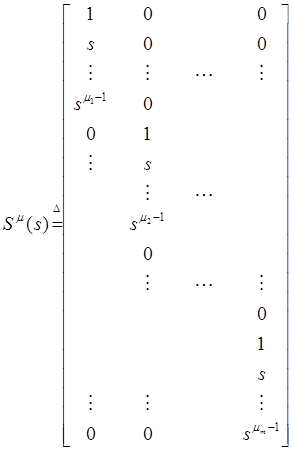 (8)
(8)
тогда
![]() (9)
(9)
Подстановка z(s) из (6) в (9) дает
![]()
а из (7) следует, что
![]() .
.
откуда
![]()
Ввиду того, что последнее
равенство справедливо при ![]() , получаем
, получаем
![]() (10)
(10)
Здесь матрица ![]() имеет размеры
имеет размеры ![]() Тогда СIможет быть
определена как единственная
Тогда СIможет быть
определена как единственная ![]() вещественная матрица
(содержащая в каждой строке единственный ненулевой единичный элемент) такая,
что
вещественная матрица
(содержащая в каждой строке единственный ненулевой единичный элемент) такая,
что
![]() (11)
(11)
Смысл (11) легко увидеть,
если (10) умножить слева на СIи учесть
(11): ![]() Здесь слева представлено правое
полиномиальное разложение передаточной функции
Здесь слева представлено правое
полиномиальное разложение передаточной функции ![]() . Тогда
из (9) и (11) следует
. Тогда
из (9) и (11) следует
![]() (12)
(12)
и тройке А, В и СI , соответствующая описанию в пространстве состояний, действительно реализует P-1(s), т.е.
![]() (13)
(13)
Вернемся к соотношению
![]()
Матричная передаточная
функция, представленная правым полиномиальным разложением ![]() , равна правой части последней формулы. Мы
далее отметим, что
, равна правой части последней формулы. Мы
далее отметим, что ![]() раз продифференцировав (12) и
использовав (7), где
раз продифференцировав (12) и
использовав (7), где ![]() – некоторое еще не определенное
целое, получим соотношение:
– некоторое еще не определенное
целое, получим соотношение:
![]()
![]()
![]()
![]()
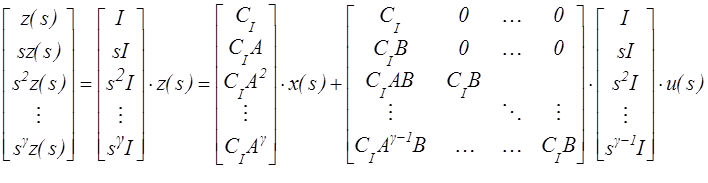 (14)
(14)
![]()
![]()
![]()
![]()
Действительно:
![]() ,
,
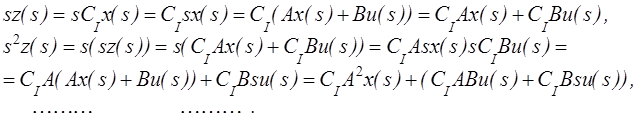
В свете (5) и (9) и определений, связанных с каждой из матриц (14), мы сейчас имеем
![]() (15)
(15)
Из-за справедливости (15) для любых значений z(s) следует, что
![]() (16)
(16)
Это соотношение ключевое в данной методике. Интересно отметить, что (16) получено из известного P(s) посредством выполнения одних лишь операций умножения над вещественными матрицами.
Если сейчас ![]() определить как степень R(s), то будет ясно, что R(s) может быть выражена как произведение однозначно
определенной вещественной
определить как степень R(s), то будет ясно, что R(s) может быть выражена как произведение однозначно
определенной вещественной ![]() матрицы
матрицы ![]() и матрицы
и матрицы ![]() , т.е.
, т.е.
![]() (17)
(17)
Умножив (16) слева на ![]() , получим
, получим
![]()
![]() (18)
(18)
Мы, наконец, отметим, что,
так как столбцовая степень ![]() меньше, чем столбцовая
степень правильной P(s), т.е. что
меньше, чем столбцовая
степень правильной P(s), т.е. что
![]() (19)
(19)
матрица ![]() будет строго правильной рациональной
матрицей. Отсюда следует, что
будет строго правильной рациональной
матрицей. Отсюда следует, что ![]() должно соответствовать
единственной полиномиальной матрице
должно соответствовать
единственной полиномиальной матрице ![]() , определенной (1) и
(2), т.е.
, определенной (1) и
(2), т.е.
![]() (20)
(20)
что с учетом (18) дает
![]() (21)
(21)
Определение
![]() и
и ![]() из (20)
и (21) представляет алгоритм вычисления такой единственной пары посредством
выполнения одних умножений с использованием P(s), которая:
из (20)
и (21) представляет алгоритм вычисления такой единственной пары посредством
выполнения одних умножений с использованием P(s), которая:
1) столбцово правильная;
2) не имеет нулевых столбцовых степеней.
Может быть показано, что если какое-либо из этих условий нарушено, то посредством умножения справа матрицы P(s) на подходящим образом выбранную несингулярную полиномиальную матрицу H(s) можем получить, что P(s)H(s) будет удовлетворять как п.1, так и п.2. Далее, если R(s)H(s) затем разделить на P(s)H(s), используя приведенный выше алгоритм, частное будет равно желаемому частному, в то же время умножение справа полученного остатка на P-1(s) дает желаемый остаток, что несложно проверить.
П р и м е р. Проиллюстрируем алгоритм, рассмотрев пару полиномиальных матриц
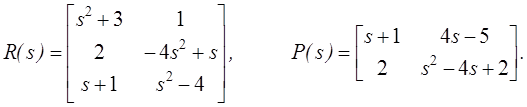
Так как P(s) столбцово
приведенная с ![]() и
и ![]() , то
, то
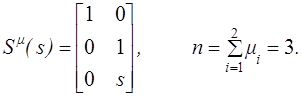
Сейчас может быть использована «структурная теорема»для получения управляемого представления в пространстве состояний, а именно
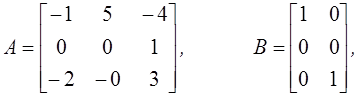
которые удовлетворяют (10). Матрица CI определяется единственным образом из (11):
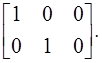
Действительно, из (11) ![]() :
:
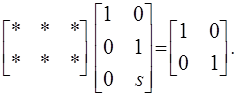
Здесь звездочками помечены элементы матрицы CI, которые подлежат определению.
П
р и м е ч а н и е. Для определения матриц А, В, С можно воспользоваться
процедурой, изложенной в МПФ $18 (обозначения оттуда же). Воспользуемся правым
полиномиальным разложением ![]() известной передаточной
матричной функции
известной передаточной
матричной функции ![]() Из P(s) определяем:
Из P(s) определяем:
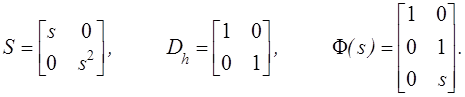
Из уравнения
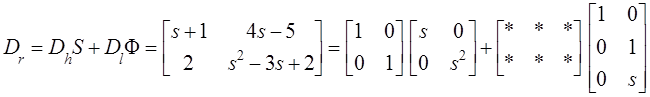
найдем ![]() :
:
![]()
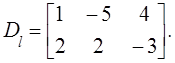
Кстати, из ![]() (
(![]() –
единичная матрица) несложно найти
–
единичная матрица) несложно найти ![]() .
.
Развернем уравнение ![]() :
:
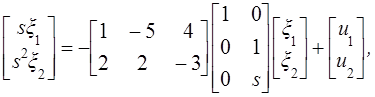
откуда
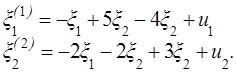
Так как ![]() :
:
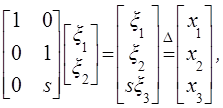
то ![]() что
позволяет преобразовать дифференциальные уравнения относительно
что
позволяет преобразовать дифференциальные уравнения относительно ![]() к виду
к виду
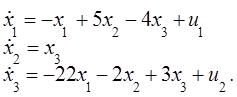
Матрицы А, В найдены. ▄
Матрицы ![]() и
и ![]() , определенные в (14), можно вычислить,
используя тройку (А, В, С) с
, определенные в (14), можно вычислить,
используя тройку (А, В, С) с ![]() , т.е. в данном примере
, т.е. в данном примере
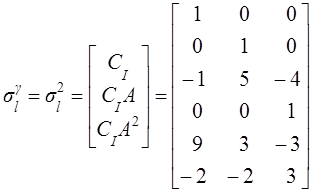
и
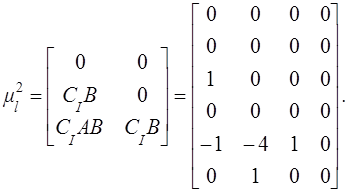
В свете (17) (![]() найдем
найдем ![]() :
:
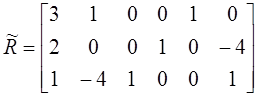
из уравнения

Тогда
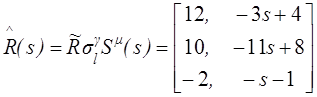
и
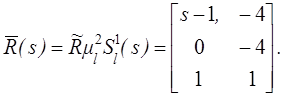
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.