Аппроксимация функций

                                Министерство образования РФ

НГТУ

Расчетно-графическая работа

Аппроксимация функций

Факультет  АВТ                                                           Преподаватель

Группа:      АП-018                                                       Чикильдин  Г.П.  

Студент:     Лазня Д. В.                                                                                    

Вариант:     7                                                                                         

Новосибирск

2002

I.  Постановка задачи.

На интервале [a,b] произвести аппроксимацию реализации функцииf(t), заданной на [a,b] с шагом Dt, обобщенным рядом Фурье по системе ортогональных (ортонормированных) на [a,b] с весом r(t) базисных функций y_r(t),  r=1,2,…,L.

Определить на [a,b] погрешности аппроксимации.

Проанализировать влияние числа L учитываемых членов ряда Фурье, на точность аппроксимации, изменяя параметр L от

L _min =3 до L _max =7 с шагом DL=1.

Вид аппроксимируемой функцииCOS(2*t);

Интервал  [a,b]=[0,75;2,35];

Шаг Dt=0.025;

Базисные функции – Тригонометрические функции.

II.  Листинг головной программы.

Program kursovic

Dimension t(65),F(65),F1(65),GC(7,65),GS(7,65),AG(7),BG(7)

Dimension E(65),N(5),FF(65),FF1(65),FF3(65),FF5(65),G(7,65)

Dimension E1(65),E3(65),E5(65)

C     F(t)=COS(2*t) basic=TRIGONOMETR

WRITE(1,197)

WRITE(1,198)

A=0.75

B=2.35

DT=0.025

KON=(B-A)/DT+1

DO 18 I=1,KON

t(I)=A+DT*(I-1)

F(I)=COS(2*t(I))

IF (I.LT.6) N(I)=I

18    CONTINUE

WRITE (4,240)

DO 11 L=1,7

CALL N1YTPG(A,B,KON,DT,L,GC,GS)

CALL N1YKFG(A,B,KON,F,F1,DT,L,AG,BG)

CALL N1YWFG(KON,L,AG,BG,GC,GS,FF)

CALL N1YEEE(F,FF,KON,E,EM,ES,EP,EMO,ESO,EPO)

WRITE (4,241) L,EMO,ESO

IF (L.EQ.1) THEN

DO 1 NUM=1,KON

FF1(NUM)=FF(NUM)

E1(NUM)=E(NUM)

1     CONTINUE

ENDIF

IF (L.EQ.3) THEN

DO 3 NUM=1,KON

FF3(NUM)=FF(NUM)

E3(NUM)=E(NUM)

3     CONTINUE

ENDIF

IF (L.EQ.5) THEN

DO 5 NUM=1,KON

FF5(NUM)=FF(NUM)

E5(NUM)=E(NUM)

5     CONTINUE

ENDIF

WRITE (1,200)

DO 2 K=1,L

WRITE (1,201) K,AG(K),BG(K)

2     CONTINUE

WRITE (1,205)

DO 19 I=1,KON

WRITE (1,206) t(I),F(I),FF(I),E(I)

19    CONTINUE

11    CONTINUE

WRITE (1,210) (N(I),I=1,5)

DO 22 I=1,KON

DO 28 KK=1,L

G(KK,I)=GC(KK,I)+GS(KK,I)

28    CONTINUE

WRITE (1,211) t(I),(G(K,I),K=1,5)

WRITE (3,211) t(I),(G(K,I),K=1,5)

22    CONTINUE

WRITE (2,220)

DO 23 IK=1,KON

WRITE (2,221) t(IK),F(IK),FF1(IK),FF3(IK),FF5(IK)

WRITE (5,221) t(IK),E1(IK),E3(IK),E5(IK)

23    CONTINUE

197   format(/,'LAZNYA DENIS VALERIEVICH AP-018 VARIANT - 7',/)

198   format(/,'A=0.75 B=2.35 DT=0.025 F(t)=COS(2*t) TRIGONOMETR',/)

200   format(//,2X,'L',4X,'AG',8X,'BG')

201   format(2X,I1,2(F11.5))

205   format(//,2x,'t=',8x,'F(t)=',8X,'~F(t)=',8X,'e(t)=')

206   format(2x,f4.2,3(2x,f11.6))

210   FORMAT(//,2X,'t(I)',5(6X,'FI(',I1,')'))

211   FORMAT(2X,F4.2,2X,5(2X,F9.6))

220   FORMAT(2X,'t=',8X,'F(I)',7X,'FF1=',7X,'FF3=',7X,'FF5=')

221   FORMAT(2X,F4.2,2X,4(2X,F9.6))

240   FORMAT(2X,'L=',7X,'EMO=',10X,'ESO=')

241   FORMAT(2X,I2,2X,2(2X,E13.6))

end

III.  Графики зависимостей

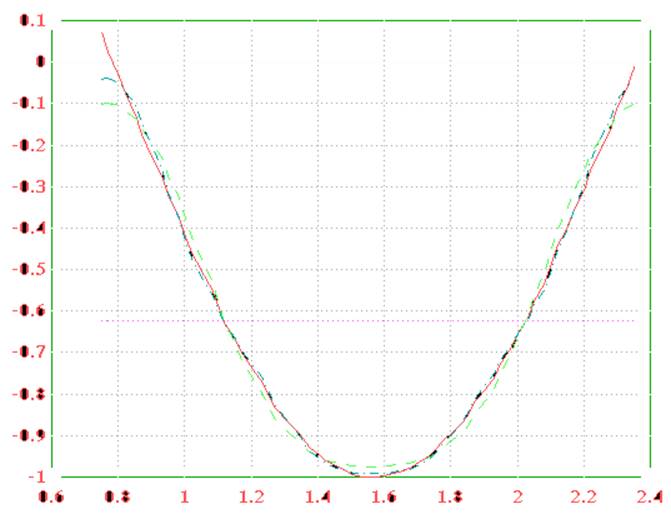
1) f(t); ~fi(t), где i – число учитываемых членов ряда Фурье

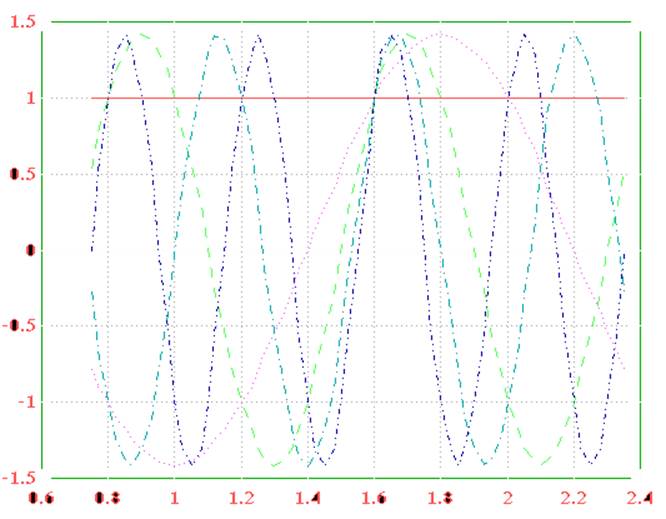
2) ~y_r(t);r(t)

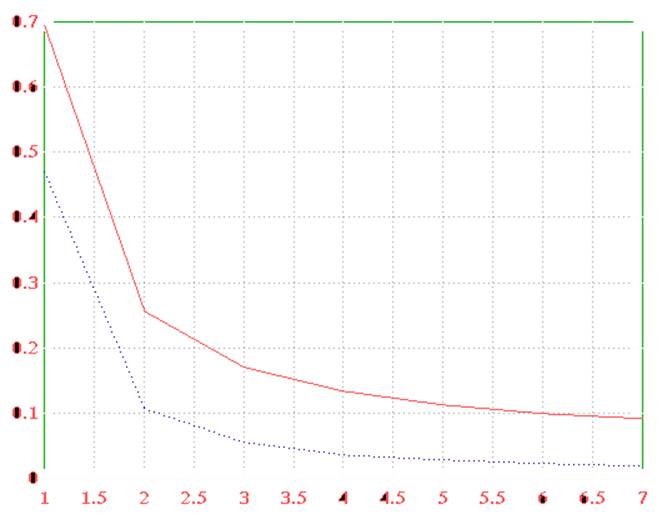
3)е_мо(L),е_со(L),L-число учитываемых членов ряда Фурье

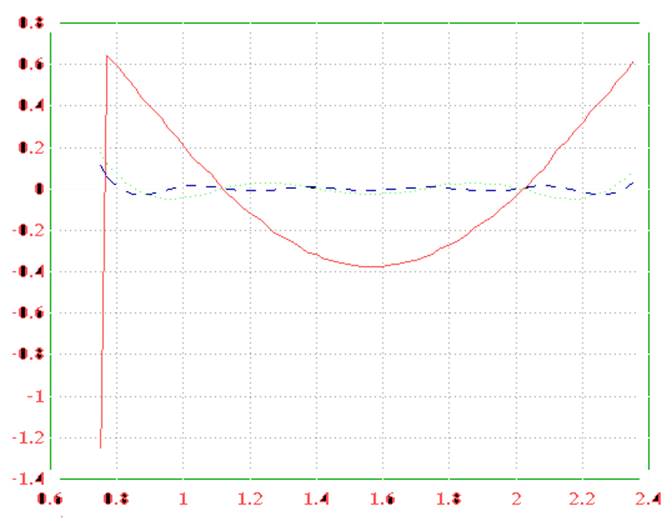
4) Er(T), r=1,3,5

V. Выводы по результатам работы

Погрешность аппроксимации , с учетом большего числа членов ряда Фурье, имеет меньшее значение, но при некотором L начинает возрастать в связи с накоплением арифметической погрешности вычисления.