Анализ и синтез механизмов сенного пресса, страница 6

Из условия сборки получим: 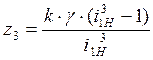                                                        (4.9)

Используя (4.9) и заданное передаточное отношение, получим:

.

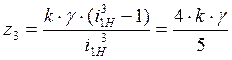Подбирая числа сателлитов от 3 до 6 и учитывая, что  - целое число, получим искомые числа зубьев колеса 3, которые должны лежать в пределах от 85 до 150, поскольку зацепление колеса 3 и сателлита 2 – внутреннее.

 В итоге получим таблицу 4.2, в которой помещены числа зубьев колеса 3 при различных значениях   и k.

Таблица 4.2                     Числа зубьев колеса 3

Далее решаем совместно уравнения и получаем систему уравнений, из которой определяем остальные числа зубьев.

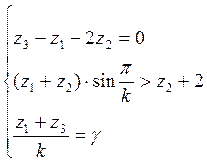
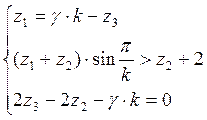
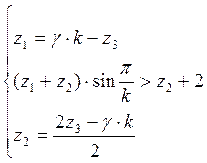                      (4.10)

Из системы (4.10) находим числа зубьев колеса 1 и колеса 2 для разных значений k и для найденных величин  (таблица 4.3). Эти значения лежат в пределах от 17 до 150.

                              Таблица 4.3                              Числа зубьев колес 1 и 2

Для того, чтобы выбрать приемлемый вариант, проверяем выполнение условие соседства (4.8).

          Согласно этому условию, варианты для числа сателлитов, равного 5 и 6, не подходят. Поэтому из всех вариантов выбираем тот, который будет иметь наименьшие габариты. По данному расчету подходит вариант, для которого .

          Для проверки правильности полученного результата определяем передаточное отношение зубчатого механизма. Общее передаточное отношение зубчатого механизма равно произведению передаточных отношений планетарной ступени и пары зубчатых колес 4 и 5:

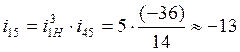. Знак минус указывает на то, что колеса 4 и 5 вращаются в противоположных направлениях.

4.2.2. Графический метод решения

Далее проверяем полученный результат с помощью графического метода. Для его проведения выбираем масштабный коэффициент 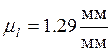 и вычерчиваем кинематическую схему механизма (рис. 4.2 а)).

Графический метод состоит в построении планов линейных и угловых скоростей.

4.2.2.1. Построение плана линейных скоростей

Проводим параллельно структурной схеме механизма линию нулевых скоростей OO^/. На эту линию проецируем все характерные точки исходного механизма. Проекции этих точек обозначаем соответствующими малыми буквами латинского алфавита. Далее строим график распределения линейных скоростей механизма (рис.4.2 б))

Рассматриваем движение точки C. Скорость данной точки определится как , где - угловая скорость водила. Из точки c проводим отрезок произвольной длины и получаем точку c^/. Точка B принадлежит и сателлиту 2, и звену 3, поэтому скорость ее равна 0. Соединяем точку b и точку c^/. Полученная линия представляет собой распределение линейных скоростей по звену 2. Из точки d проводим линию до пересечения с линией bc^/, получим точку d^// .

Далее рассматриваем распределение линейных скоростей по звену 1.

Для этого точку a, лежащую на линии OO^/, соединяем с точкой c^/. Линия ac^/ показывает распределение линейных скоростей по звену 1.

Соединяя точку d^// с точкой a, получаем распределение линейных скоростей по звену 4 и водилу. Из точки e, лежащей на OO^/, проводим отрезок ee^/ до пересечения с линией ad^//. Полученную точку соединяем с точкой d^/ и находим распределение скоростей по звену 5.

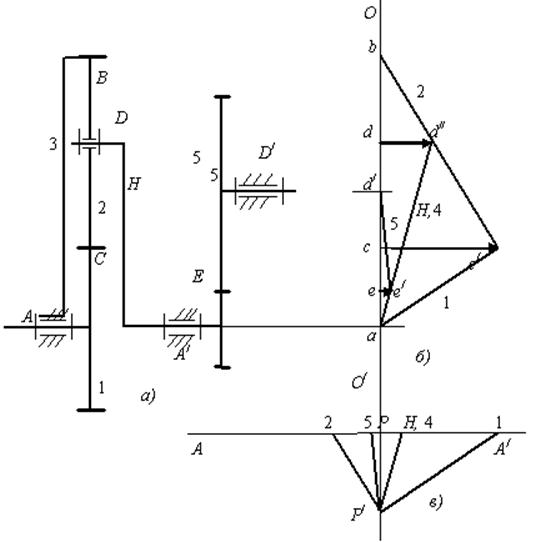
Рис. 4.2. Построение планов линейных и угловых скоростей

4.2.2.2. Построение плана угловых скоростей

Проводим горизонтальную линию AA^/, перпендикулярную линии OO^/, и получаем точку P. От данной точки откладываем вниз произвольный отрезок и обозначаем точкой P^/ его конец (рис.4.2 в)). Далее от точки P^/ проводим линии, параллельные линиям распределения линейных скоростей и в точках их пересечения с линией AA^/ ставим соответствующие обозначения.

Тогда передаточное отношение при неподвижном 3 колесе определяется так:

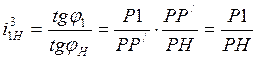                                               (4.11)

В выражении (4.11)  - угол между прямыми  и , а угол  - между прямыми и .

Тогда согласно этому выражению и (рис.4.2 в)) получим: .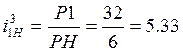

Общее передаточное отношение всего механизма определится по формуле, аналогичной (4.11): 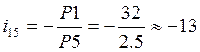. Знак минус берем потому, что исследуемые отрезки находятся по разные стороны от оси .

4.3. Результат решения

Таким образом, в результате решения поставленной задачи разными методами были получены передаточные отношения для зубчатого механизма. Величины передаточных отношений для графического и аналитического методов практически совпадают.

Оглавление

                                                                                                         Стр.

     1. Структурный анализ механизмов                                       2

     2. Кинематический анализ механизмов                                  7

 3. Силовой анализ                                                                     17

 4. Синтез планетарной передачи                                             27