Анализ и синтез механизмов сенного пресса, страница 5

3.3.1 Силовой анализ структурной группы 4 – 5

Рисуем структурную группу 4 – 5 и прикладываем к ней все действующие силы и моменты. Реакции  и  изображаем разложенными на нормальную  и касательную  составляющие.

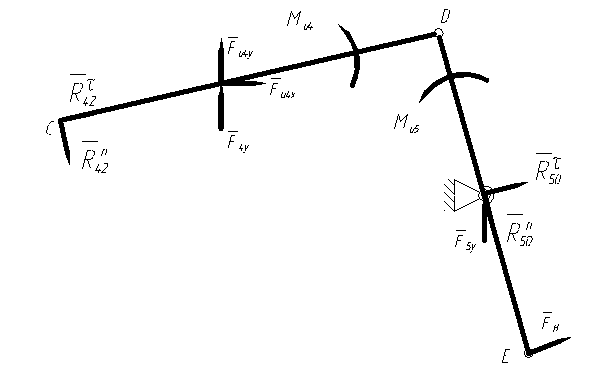
Силовой анализ группы начинаем с определения касательных составляющий реакций, для чего составляем уравнение моментов относительно точки D для звена 4 и звена 5:

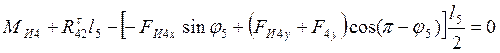
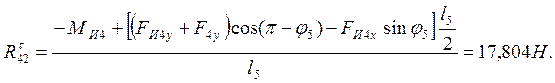
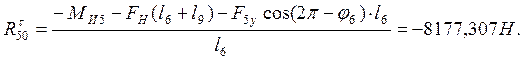
Запишем векторное уравнение сил, действующих на эту группу в целом, таким образом, чтобы неизвестные реакции находились по краям:

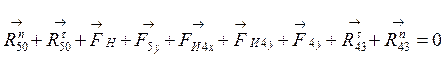                     (5.3)

Уравнение (5.3) решаем графическим методом построения планов сил. Выбираем масштабный коэффициент сил . Находим для известных сил величины отрезков, которыми они изображаются на плане сил:

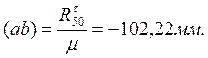
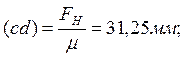
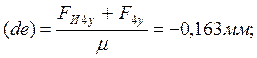
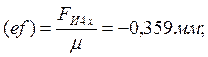
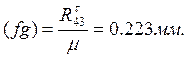
Последовательно, начиная с ab, откладываем на плане сил векторы, изображающие силы. Через точку a проводим линию действия реакции  перпендикулярную , а через точку g – реакцию . Точка е пересечения этих линий определит отрезки eh и bh, которые изображают искомые реакции. Истинные величины реакций находим следующим образом:

Данные, полученные в результате расчетов графическим и аналитическим методом, приведены в табл. 5.2.

Таблица 5.2

Результаты силового анализа структурной группы 4 – 5

Величина	, Н	, Н
Графически	5954,40	8279,20
Аналитически	5954,49	8279,12
Отклонение, D, %	0,002	0,001

3.3.2 Силовой анализ структурной группы 2 – 3

Рисуем структурную группу 2 – 3 и прикладываем к ней все действующие силы и моменты.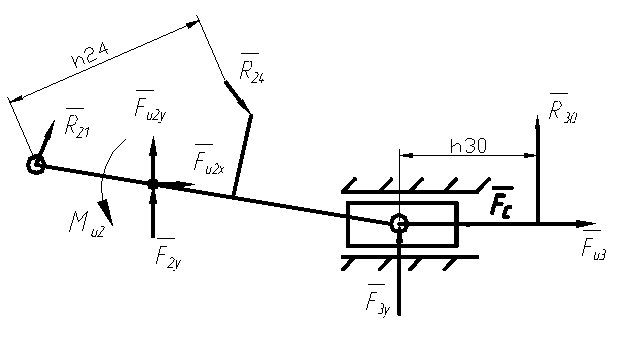

Силовой анализ группы начинаем с определения реакции , для чего составляем уравнение моментов относительно точки А для звеньев 2 и 3:

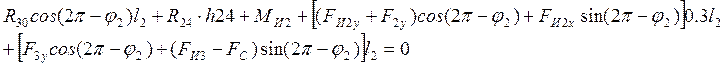
Длины плеч берем из плана положений механизма. Решив последнее уравнение, найдем:

Составляем векторное уравнение сил, действующих на группу 2 – 3 в целом. Уравнение записываем таким образом, чтобы неизвестные величины находились по краям:

Выбираем масштабный коэффициент сил . Находим для известных сил величины отрезков, которыми они изображаются на плане сил:

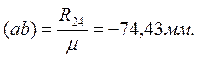
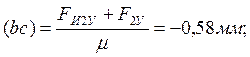
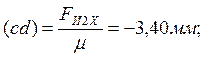
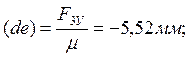
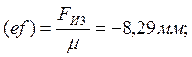
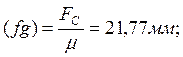
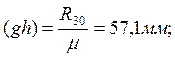
Последовательно, начиная с отрезка (ab), откладываем остальные отрезки в соответствии с векторным уравнением сил. Отрезок (ah) изображает реакцию . Истинное значение этих реакций определится:

;

Данные, полученные в результате расчетов графическим и аналитическим методом, приведены в табл. 5.3.

Таблица 5.3

Результаты силового анализа структурной группы 2 – 3

Величина	, Н	, Н
Графически	3412	4569,072
Аналитически	3411,36	4569,11
Отклонение, D, %	0	0

3.3.3 Силовой анализ начального звена

Прикладываем к начальному звену все силы и моменты. Здесь  – уравновешивающий момент, а .

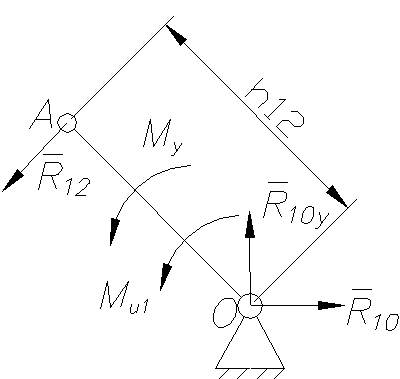
Запишем уравнение суммы моментов относительно точки О:

откуда

Находим погрешности определения уравновешивающего момента :

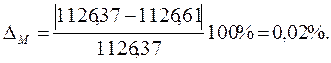
ссс

4. СИНТЕЗ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ

Синтез планетарной передачи состоит в подборе чисел зубьев колес и числа сателлитов по заданной схеме и заданному передаточному отношению.

4.1. Исходные данные

На рис. 4.1. показана структурная схема зубчатого механизма, а в таблице 4.1. приведены исходные данные для расчетов.

Величина	Значение
z4	14
z5	36
	5

Таблица 4.1.  Исходные данные       

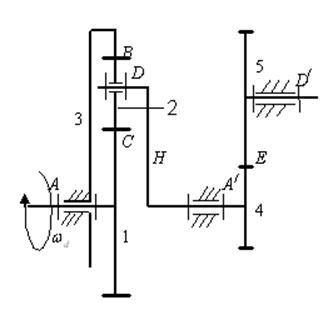
              Рис. 4.1. Зубчатый механизм

          4.2. Метод решения

          4.2.1. Аналитический метод определения чисел зубьев колес по заданному передаточному отношению

Для определения передаточного отношения всем звеньям планетарного механизма мысленно сообщается дополнительная угловая скорость . В результате получим механизм, у которого оси всех колес неподвижны. Такой механизм называется обращенным.

Для такого механизма угловые скорости определяются соответственно:

                                                         (4.1)

          Передаточное отношение обращенного механизма:

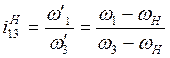                                                    (4.2)

В реальном механизме . С учетом этого обстоятельства (4.2) примет вид:

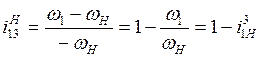                                               (4.3)

В выражении (4.3)  - передаточное отношение планетарного механизма от звена 1 к звену H при неподвижном звене 3.

Из формулы (4.3) найдем, что передаточное отношение исследуемого механизма определится

                                                       (4.4)

Также передаточное отношение  для обращенного механизма (механизма, у которого оси неподвижны) можно определить таким образом:

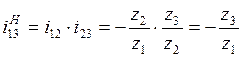                                                  (4.5)

Подставляя (4.5) в (4.4), получим .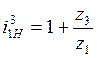

При решении задачи используются условия соосности, сборки и соседства. Их выводим, исходя из предложенной схемы планетарного механизма (рис. 4.1). Кроме того, числа зубьев должны находиться в пределах от 17 до 150.

Условие соосности требует, чтобы расположение осей солнечного, опорного колеса и водила на одной прямой обеспечивалось зацеплением сателлитов с этими колесами.

В нашем случае

                                         (4.6)

Уравнение сборки получаем из необходимости того, чтобы зубья всех сателлитов вошли во впадины центральных колес:

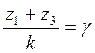                                                      (4.7)

Здесь k – число сателлитов, выбираемое в пределах от 3 до 6,  - любое целое число.

Условие соседства требует, чтобы соседние сателлиты разных механизмов не задевали друг друга. Этому утверждению соответствует следующее выражение:

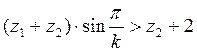                                               (4.8)

Решая совместно уравнения (4.6)-(4.8), получим искомые числа зубьев колес, обеспечивающих заданное передаточное отношение.